 por rhodry » Seg Dez 05, 2011 21:04
por rhodry » Seg Dez 05, 2011 21:04
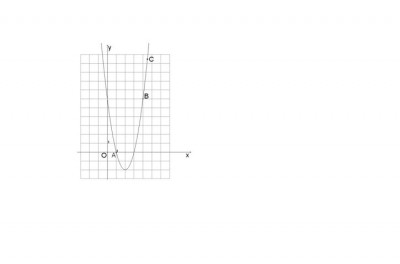
o gráfico segue em anexo:
O gráfico que segue representa uma função polinomial f, do segundo grau. Os pontos
A = (1, 0), B = (4, 6) e C = (4,5, 10,5) pertencem a esse gráfico.
a) Determine a lei de formação de f.
- Anexos
-
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Rosana Vieira » Seg Dez 05, 2011 22:52
por Rosana Vieira » Seg Dez 05, 2011 22:52
Olá rhodry, você já resolveu o exercício 1a e 1b e você pode me ajudar a terminar 1b)| x – y | = 3
x – y = 3
x = 3 + y
y = 3 – x
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por ivanilda » Seg Dez 05, 2011 23:22
por ivanilda » Seg Dez 05, 2011 23:22
Oi rhodry, meu nome e Ivanilda, também faço o redefor.... pensei em comecar a resolver por matrizes e determinantes.....acredito ser este o caminho...
-
ivanilda
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Dez 05, 2011 23:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
 por vanessa_mat » Ter Dez 06, 2011 00:05
por vanessa_mat » Ter Dez 06, 2011 00:05
rhodry escreveu:o gráfico segue em anexo:
O gráfico que segue representa uma função polinomial f, do segundo grau. Os pontos
A = (1, 0), B = (4, 6) e C = (4,5, 10,5) pertencem a esse gráfico.
a) Determine a lei de formação de f.
comecei achando Y= ax^2 +bx+c o c é onde corta no eixo y
temos dois valores para montar um sistema: A( 1,0), substitui o valor de x e de y na expressão, depois substitui B( 4,6) tb na expressão, fica ~dois sistemas em função de a e b. Acha o a e o b e substitui na formação y = ax^2 +bx +c. Espero ter ajudado.
Quanto ao exercício 1 se alguém puderme dar uma ajudar??? em falar em ajuda alguém do redefor de matemática conseguiu começar o exercício da DE???
-
vanessa_mat
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Nov 21, 2011 16:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por Wanzinha » Ter Dez 06, 2011 00:15
por Wanzinha » Ter Dez 06, 2011 00:15
Rosana...veja se é isso?
na 1b m2 apliquei a definição de modulo e achei { (3+y,x-3)e(-3+y,x+3)}
-
Wanzinha
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Out 24, 2011 02:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por rhodry » Ter Dez 06, 2011 18:40
por rhodry » Ter Dez 06, 2011 18:40
Exe1
olá colegas, desenvolvi atribuindo valores para x e y, donde a sua soma terá que ser igual 1, perceberemos que poderemos encontrar vários pontos ordenados.
exemplo:
x + y = 1
-2+1=1
x - y = 1
4-3=1
-x + y = 1
-5+6=1
-x - y = 1
-5-(-6)=1
........
Percebe que teremos infinitos pontos?
Se quiserem compartilhar e-mail:
rhodry_jr@hotmail.comEditado pela última vez por
rhodry em Ter Dez 06, 2011 18:45, em um total de 1 vez.
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por rhodry » Ter Dez 06, 2011 18:42
por rhodry » Ter Dez 06, 2011 18:42
Rosana Vieira escreveu:Olá rhodry, você já resolveu o exercício 1a e 1b e você pode me ajudar a terminar 1b)| x – y | = 3
x – y = 3
x = 3 + y
y = 3 – x
olá Rosana me mande um e-mail:
rhodry_jr@hotmail.com
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por 1000ton » Qui Dez 08, 2011 21:31
por 1000ton » Qui Dez 08, 2011 21:31
rhodry escreveu:Rosana Vieira escreveu:Olá rhodry, você já resolveu o exercício 1a e 1b e você pode me ajudar a terminar 1b)| x – y | = 3
x – y = 3
x = 3 + y
y = 3 – x
olá Rosana me mande um e-mail:
rhodry_jr@hotmail.com
x dc
-
1000ton
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Nov 06, 2011 08:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por ted41 » Qui Dez 08, 2011 22:43
por ted41 » Qui Dez 08, 2011 22:43
f(x) = ax² + bx + c
Sub. A (1, 0) temos:
(1) a + b + c = 0
Sub. B (4, 6) temos:
(2) 16a + 4b + c = 6
Para C (9/2, 21/2)
(3) 81a + 18b + 4c = 42
Logo teremos um sistema de três equações com três incógnitas
a + b + c = 0
16a + 4b + c = 6
81a + 18b + 4c = 42
Resolvendo o sistemas temos que a = 2, b = -8 e c = 6, assim f(x) = 2x² - 8x + 6.
b) (2,5) Determine as coordenadas do vértice dessa parábola
xv = - b/2a
xv = 2
yv = 2 . 22 – 8. 2 + 6
yv = - 2
As coordenadas do vértice dessa parábola é (2, -2)
De uma olhada eu fiz dessa forma
A primeira eu ainda não fiz se alguém tiver um ideia por favor acenda a luz
Editado pela última vez por
ted41 em Qui Dez 08, 2011 22:56, em um total de 3 vezes.
-
ted41
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Nov 17, 2011 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por ted41 » Qui Dez 08, 2011 22:45
por ted41 » Qui Dez 08, 2011 22:45
A primeira eu ainda não fiz se alguém tiver um ideia por favor acenda a luz
-
ted41
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Nov 17, 2011 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.












