 por Wanzinha » Sáb Dez 03, 2011 19:35
por Wanzinha » Sáb Dez 03, 2011 19:35
Identifique o conjunto dos pontos (x, y) tais que:
| x | + | y | = 1
então eu comecei assim:
De |x|+ |y|= 1 temos que |y|=1-|x|, mas 1-|x|> ou = 0, assim devemos ter que:
1-|x|> ou = 0
-|x|> ou = -1 (x -1)
|x|< ou = 1
Mas |x|< ou = 1 ; -1 < ou = x < ou = 1. Com isso vemos que teremos que
analisar o valor de y apenas para o caso em que -1 < ou = x < ou = 1.
será isso??
-
Wanzinha
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Out 24, 2011 02:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por joaofonseca » Sáb Dez 03, 2011 21:13
por joaofonseca » Sáb Dez 03, 2011 21:13
Intuitivamente, é facíl de observar que quaisquer que sejam os valores que y e x tomem o valor absoluto devolve sempre valores positivos.Logo quais são os dois números positivos cuja soma é igual a um?
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funçao modular
por Fiel8 » Sex Jul 10, 2009 19:25
- 1 Respostas
- 2614 Exibições
- Última mensagem por Molina

Sex Jul 10, 2009 21:50
Funções
-
- Função Modular
 por geriane » Sáb Abr 03, 2010 21:32
por geriane » Sáb Abr 03, 2010 21:32
- 3 Respostas
- 3113 Exibições
- Última mensagem por Molina

Dom Abr 04, 2010 12:57
Funções
-
- Funçao modular
 por Skcedas » Qua Mai 26, 2010 19:29
por Skcedas » Qua Mai 26, 2010 19:29
- 6 Respostas
- 5361 Exibições
- Última mensagem por netlopes

Ter Jun 08, 2010 18:11
Funções
-
- Função Modular
 por DanieldeLucena » Seg Set 20, 2010 18:03
por DanieldeLucena » Seg Set 20, 2010 18:03
- 1 Respostas
- 2236 Exibições
- Última mensagem por MarceloFantini

Seg Set 20, 2010 19:35
Funções
-
- Função Modular
por Pri Ferreira » Ter Nov 22, 2011 18:20
- 1 Respostas
- 1869 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 18:56
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



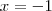 e
e  atende as condições, ou mesmo
atende as condições, ou mesmo  ,
,  , logo não são apenas números positivos admitidos. A questão tem de ser avaliada em quatro casos:
, logo não são apenas números positivos admitidos. A questão tem de ser avaliada em quatro casos: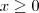 e
e 

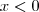 e
e 

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
