 por Richard Oliveira » Sáb Nov 12, 2011 14:59
por Richard Oliveira » Sáb Nov 12, 2011 14:59
AOlá, estou tentando resolver alguns exercícios sobre funções em uma apostila. Encontrei uma questão a qual não bate com o meu resultado. Segue:
Sejam f: R em R e g: R em R duas funções dadas por
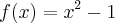
e
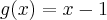
. A diferença entre as funções compostas

é igual a:
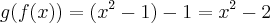
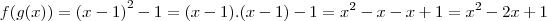
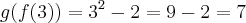
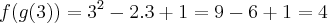
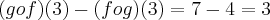
Como vocês podem ver, nas minhas contas o resultado é 3, porém no gabarito da apostila o resultado é 4. O que está errado?
-
Richard Oliveira
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Nov 04, 2011 16:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Richard Oliveira » Sáb Nov 12, 2011 17:04
por Richard Oliveira » Sáb Nov 12, 2011 17:04
Alguém me ajuda por gentileza? Eu só quero saber se eu fiz alguma coisa errada ou não, se puderem me responder eu ficaria muito agradecido.
-
Richard Oliveira
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Nov 04, 2011 16:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sáb Nov 12, 2011 23:23
por MarceloFantini » Sáb Nov 12, 2011 23:23
O que está errado é aqui:
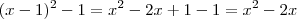
. Tente refazer.
Em tempo: suas mensagens tem apenas 2 horas de diferença.
Quando pedir por ajuda, espere, somos todos voluntários e não passamos o dia no fórum.Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Richard Oliveira » Seg Nov 14, 2011 00:50
por Richard Oliveira » Seg Nov 14, 2011 00:50
Entendi, eu estava pulando uma parte no exercício.
Eu entendo e sei que vocês não passam o dia inteiro aqui, e já quero deixar bem claro: eu não estou achando que vocês são obrigados a fazer serviços pra mim, por isso que eu procuro ser o mais educado possível em minhas perguntas. Eu estou aqui no site perguntando, porque já é um site próprio para isso, e como eu tenho um sonho que desejo realizar, estou aqui tentando tirar minhas dúvidas. Em relação a meu segundo post, eu postei aquele comentário porque eu vi outro tópico mais novo sendo respondido antes do que o meu. Mas antes de mais nada, eu ressalto que quero ter uma boa relação no site, portanto eu serei humilde: mesmo não sendo respondido antes, acredito que eu devia ter esperado mais e assim farei nós próximos tópicos.
Obrigado pela resposta, consegui resolver.
-
Richard Oliveira
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Nov 04, 2011 16:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Tentei, mas nao bate o resultado.
por Liliani » Qua Abr 07, 2010 17:05
- 1 Respostas
- 4175 Exibições
- Última mensagem por estudandoMat

Qua Abr 07, 2010 17:37
Desafios Fáceis
-
- trigonometria simples mas o resultado não bate certo.
 por tiagofe » Sex Mai 06, 2011 17:31
por tiagofe » Sex Mai 06, 2011 17:31
- 4 Respostas
- 5206 Exibições
- Última mensagem por claudinho

Dom Jun 12, 2011 12:20
Trigonometria
-
- [Função composta]Achar o dominio de uma função composta
por lucasmath » Dom Abr 12, 2015 16:09
- 0 Respostas
- 2229 Exibições
- Última mensagem por lucasmath

Dom Abr 12, 2015 16:09
Funções
-
- Função inversa [Gabarito não fecha de jeito algúm]
por Matheus Lacombe O » Qui Set 06, 2012 00:37
- 3 Respostas
- 2566 Exibições
- Última mensagem por MarceloFantini

Qui Set 06, 2012 19:06
Funções
-
- [Função Exponencial] - Resultado
por Rike Morais » Sáb Jul 09, 2016 00:23
- 1 Respostas
- 1887 Exibições
- Última mensagem por DanielFerreira

Sáb Jul 09, 2016 12:26
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
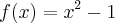 e
e 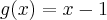 . A diferença entre as funções compostas
. A diferença entre as funções compostas é igual a:
é igual a: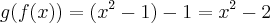
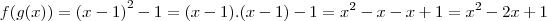
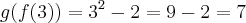
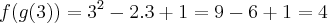
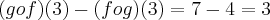

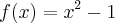 e
e 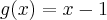 . A diferença entre as funções compostas
. A diferença entre as funções compostas é igual a:
é igual a: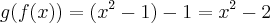
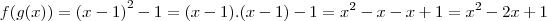
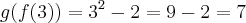
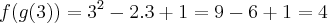
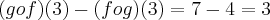


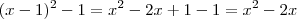 . Tente refazer.
. Tente refazer.

