 por bira19 » Ter Out 04, 2011 21:25
por bira19 » Ter Out 04, 2011 21:25
-
bira19
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 03, 2011 20:41
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em eletronica
- Andamento: formado
 por MarceloFantini » Ter Out 04, 2011 21:50
por MarceloFantini » Ter Out 04, 2011 21:50
Aplique a distributiva do lado direito e fala igualdade de coeficientes, lembrando que

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por bira19 » Ter Out 04, 2011 22:13
por bira19 » Ter Out 04, 2011 22:13
MarceloFantini escreveu:Aplique a distributiva do lado direito e fala igualdade de coeficientes, lembrando que

.
aplicandoa distributiva
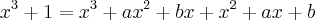
, minha duvida e como somar os termos para desmonstrar a igualdade.
-
bira19
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 03, 2011 20:41
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em eletronica
- Andamento: formado
 por MarceloFantini » Ter Out 04, 2011 22:21
por MarceloFantini » Ter Out 04, 2011 22:21
Basta juntar para formar um polinômio:
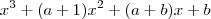
e iguale os coeficientes.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por bira19 » Ter Out 04, 2011 22:43
por bira19 » Ter Out 04, 2011 22:43
MarceloFantini escreveu:Basta juntar para formar um polinômio:
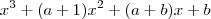
e iguale os coeficientes.
Obrigado, igualando os coeficientes encontrei
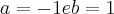
-
bira19
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 03, 2011 20:41
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em eletronica
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Por favor como se proceda para calcular esse calculo:
por andersontricordiano » Qui Mar 31, 2011 15:42
- 1 Respostas
- 2152 Exibições
- Última mensagem por DanielFerreira

Qui Mar 31, 2011 17:25
Cálculo
-
- Prove para todo n natural
por Cleyson007 » Sáb Abr 28, 2012 17:14
- 4 Respostas
- 2368 Exibições
- Última mensagem por Cleyson007

Sáb Abr 28, 2012 18:23
Cálculo: Limites, Derivadas e Integrais
-
- [Indução] Prove para todo n inteiro
por +danile10 » Qua Fev 13, 2013 19:46
- 1 Respostas
- 1716 Exibições
- Última mensagem por +danile10

Qua Fev 13, 2013 20:05
Conjuntos
-
- [Indução] Para todo n maior igual que 2
por +danile10 » Dom Fev 17, 2013 13:07
- 2 Respostas
- 1981 Exibições
- Última mensagem por e8group

Dom Fev 17, 2013 14:40
Lógica
-
- Ajuda para resolver equação para calcular velocidade média
por marcorrer » Sex Fev 24, 2012 13:10
- 0 Respostas
- 3701 Exibições
- Última mensagem por marcorrer

Sex Fev 24, 2012 13:10
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 .
.

.
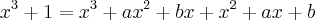 , minha duvida e como somar os termos para desmonstrar a igualdade.
, minha duvida e como somar os termos para desmonstrar a igualdade.
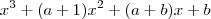 e iguale os coeficientes.
e iguale os coeficientes.

e iguale os coeficientes.
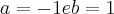

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.