 por Claudin » Qui Set 08, 2011 20:55
por Claudin » Qui Set 08, 2011 20:55
É correto afirmar que a função linear não possui inversa?
Pois nunca seria injetora, pois para ser injetora é somente se x diferente de y. tal que f(x) é diferente de f(y)
Ou seja, um único valor de x correspondente a um imagem
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qui Set 08, 2011 20:56
por MarceloFantini » Qui Set 08, 2011 20:56
Por função linear você diz

?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Qui Set 08, 2011 21:08
por Claudin » Qui Set 08, 2011 21:08
Não. Função Linear sendo f(x)= ax
Achei que todas as lineares eram f(x) = ax. No qual tem origem (0,0).
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qui Set 08, 2011 21:27
por MarceloFantini » Qui Set 08, 2011 21:27
O caso geral é
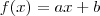
. Quando

temos o caso particular que você citou. E sim,
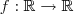
é injetora e sobrejetora, logo bijetora e portanto tem inversa.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- função linear
por marcellef » Seg Jul 12, 2010 21:30
- 1 Respostas
- 1618 Exibições
- Última mensagem por MarceloFantini

Seg Jul 12, 2010 22:10
Funções
-
- Função Linear
por Jean Cigari » Qua Jun 29, 2011 10:36
- 2 Respostas
- 1145 Exibições
- Última mensagem por LuizAquino

Qui Jun 30, 2011 13:25
Funções
-
- (UERJ) - Questão de função linear
 por Levi23 » Qua Mar 11, 2009 22:28
por Levi23 » Qua Mar 11, 2009 22:28
- 1 Respostas
- 5315 Exibições
- Última mensagem por Levi23

Qua Mar 11, 2009 22:29
Funções
-
- Questão da Uerj função linear
por gustavoluiss » Seg Fev 07, 2011 22:24
- 12 Respostas
- 7788 Exibições
- Última mensagem por Santa Lucci

Ter Fev 08, 2011 01:24
Funções
-
- Equação diferencial não-linear de função composta
 por Sally » Ter Fev 28, 2017 17:37
por Sally » Ter Fev 28, 2017 17:37
- 0 Respostas
- 2701 Exibições
- Última mensagem por Sally

Ter Fev 28, 2017 17:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





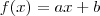 . Quando
. Quando  temos o caso particular que você citou. E sim,
temos o caso particular que você citou. E sim, 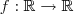 é injetora e sobrejetora, logo bijetora e portanto tem inversa.
é injetora e sobrejetora, logo bijetora e portanto tem inversa.


 .
.
 :
: