Bom dia, kael.
Você vai calcular primeiramente a

.
O resultado será um valor numérico.
Este valor encontrado vamos chamar de

.
O próximo passo é calcular o

.
O resultado se?a um valor numérico, que chamaremos de

.
Agora vamos fazer o mesmo procedimento com a outra parte da soma:
Você vai calcular primeiramente a

.
O resultado será um valor numérico.
Este valor encontrado vamos chamar de

.
O próximo passo é calcular o

.
O resultado se?a um valor numérico, que chamaremos de

.
No final precisamos somar
![f\left[g\left(\frac {1}{2} \right) \right] + g \left[f(\sqrt5 + 1) \right] \Rightarrow \beta + \theta f\left[g\left(\frac {1}{2} \right) \right] + g \left[f(\sqrt5 + 1) \right] \Rightarrow \beta + \theta](/latexrender/pictures/ca6f2673097585bd497f20c111110331.png)
Acho que com esses passos você será capaz de resolver.
Caso não consiga informe aqui que resolvo para você.
Bom estudo!


 e
e 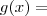 X² + 2 , determine o valor de:
X² + 2 , determine o valor de:![f\left[g\left(\frac {1}{2} \right) \right]+g \left[f(\sqrt5 + 1) \right] f\left[g\left(\frac {1}{2} \right) \right]+g \left[f(\sqrt5 + 1) \right]](/latexrender/pictures/d5c8c5409d3eb58156166e55ef89e7eb.png)


 e
e 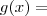 X² + 2 , determine o valor de:
X² + 2 , determine o valor de:![f\left[g\left(\frac {1}{2} \right) \right]+g \left[f(\sqrt5 + 1) \right] f\left[g\left(\frac {1}{2} \right) \right]+g \left[f(\sqrt5 + 1) \right]](/latexrender/pictures/d5c8c5409d3eb58156166e55ef89e7eb.png)

 .
. .
. .
. .
. .
. .
. .
. .
.![f\left[g\left(\frac {1}{2} \right) \right] + g \left[f(\sqrt5 + 1) \right] \Rightarrow \beta + \theta f\left[g\left(\frac {1}{2} \right) \right] + g \left[f(\sqrt5 + 1) \right] \Rightarrow \beta + \theta](/latexrender/pictures/ca6f2673097585bd497f20c111110331.png)


 , confira ai pra mim por favor!
, confira ai pra mim por favor!![f\left[g \left(\frac{1}{2} \right) \right] + f\left[g \left(\frac{1}{2} \right) \right] +](/latexrender/pictures/d31e237c7832a14db9cda2ed658bd04d.png)
![g\left[f(\sqrt5 + 1 \right] g\left[f(\sqrt5 + 1 \right]](/latexrender/pictures/fd316864c9725930f22131e72781bd73.png)

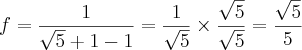







 .
.



