Já entendi como encontrar o MMC, mas como faço para encontrar se tenho números muito grandes, Exp. 250, 450?
Se fosse o 15 = 3,5, certo?
Se fosse o 30 = 5,6, certo?
E de 250? 450? Começo por onde?
Vi que a resposta é 2250.
Pensei se a resposta é 2250 então devo encontrar o MMC pegando os 250 e 450 e dividindo por um número que o resultado seja inteiro.
Peguei 250 e dividi por 5 o MMC = 5, 50
Peguei 450 e dividi por 5 o MMC= = 5, 90
Peguei o 5 x 50 x 90 = 2250. Cheguei no resultado. Mas.... meu raciocínio esta certo? É assim que devo fazer?

Muito obrigada.




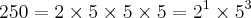

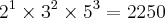



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)