Já entendi como encontrar o MMC, mas como faço para encontrar se tenho números muito grandes, Exp. 250, 450?
Se fosse o 15 = 3,5, certo?
Se fosse o 30 = 5,6, certo?
E de 250? 450? Começo por onde?
Vi que a resposta é 2250.
Pensei se a resposta é 2250 então devo encontrar o MMC pegando os 250 e 450 e dividindo por um número que o resultado seja inteiro.
Peguei 250 e dividi por 5 o MMC = 5, 50
Peguei 450 e dividi por 5 o MMC= = 5, 90
Peguei o 5 x 50 x 90 = 2250. Cheguei no resultado. Mas.... meu raciocínio esta certo? É assim que devo fazer?

Muito obrigada.




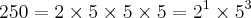

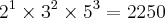




 .
.
 :
: