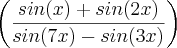
Eu fui resolvendo pelas formulas de adição e subtração, mas não deu o resultado do gabarito. Então, fui tentando resolver, de fato, eu fiz, mas não entendi muito bem o "porquê"
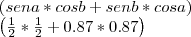
De fato, se eu cortar sen a e cos a, fico com:
![\left(\frac{1}{2}+0.87 \right)
\left(\frac{\sqrt[]{3}+1}{2} \right)](/latexrender/pictures/7aceb417f81df18a922a8357ce2e29d3.png "\left(\frac{1}{2}+0.87 \right)
\left(\frac{\sqrt[]{3}+1}{2} \right)")
No denominador, eu tenho
De fato, se eu cortar 0 e -0.87, eu fico com
Por fim,
![\left(\frac{\frac{\sqrt[]{3}+1}{2}}{-\frac{3}{2}} \right)
\left(\frac{-\sqrt[]{3}-1}{3} \right)](/latexrender/pictures/a69491fc07ba0628e7c60bf81105f59a.png "\left(\frac{\frac{\sqrt[]{3}+1}{2}}{-\frac{3}{2}} \right)
\left(\frac{-\sqrt[]{3}-1}{3} \right)")
Agradeço qualquer ajuda, desde já!
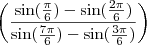
por 
.
