 por joaofonseca » Ter Mai 17, 2011 17:57
por joaofonseca » Ter Mai 17, 2011 17:57
Hoje deparei-me com um problema que não consegui decifrar a solução.
Dadas as seguintes sequências:
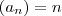
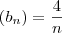

Calcule a ordem
k para a qual os termos das diferentes sequências são iguais.
Pelo que entendi tem de se achar uma ordem
k tal que
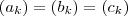
.
Eu consegui resolver graficamente, com a ajuda da máquina. Mas como faço de forma algébrica?
Obrigado.
Editado pela última vez por
joaofonseca em Ter Mai 17, 2011 18:35, em um total de 1 vez.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por joaofonseca » Ter Mai 17, 2011 18:44
por joaofonseca » Ter Mai 17, 2011 18:44
Já corrigi o erro.
FilipeCaceres escreveu:
Como passas deste conjunto de igualdades para o resultado final?
Obrigado
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por FilipeCaceres » Ter Mai 17, 2011 18:51
por FilipeCaceres » Ter Mai 17, 2011 18:51
Se

então

, similarmente se faz para o resto.
Tendo a igualdade é só substituir os valores.Seja,
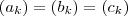
Então,
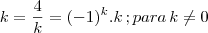
Pegando a primeira igualdade temos,
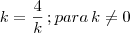
Logo,

Portanto,

Observe que ambos valores

também servem para a segunda igualdade e desta forma temos como solução os dois,ou seja.

Compreendeu?
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por joaofonseca » Ter Mai 17, 2011 19:12
por joaofonseca » Ter Mai 17, 2011 19:12
Então é como se fosse um sistema linear de três equações com 2 incógnitas!
Obrigado
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Ter Mai 17, 2011 19:33
por MarceloFantini » Ter Mai 17, 2011 19:33
Provavelmente

é natural, então a única resposta válida é

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Sequencias] Sequencias Divergentes
por RafaelPereira » Sáb Jun 08, 2013 23:34
- 2 Respostas
- 3850 Exibições
- Última mensagem por RafaelPereira

Dom Jun 09, 2013 17:53
Sequências
-
- Sequencias.
por 380625 » Qua Ago 31, 2011 02:30
- 1 Respostas
- 1875 Exibições
- Última mensagem por Renato_RJ

Qua Ago 31, 2011 13:32
Sequências
-
- sequencias
por David de Sousa » Seg Jan 30, 2012 16:23
- 2 Respostas
- 2513 Exibições
- Última mensagem por David de Sousa

Seg Jan 30, 2012 19:22
Sequências
-
- Sequencias e Séries
por Neperiano » Dom Set 26, 2010 19:28
- 1 Respostas
- 2260 Exibições
- Última mensagem por Marcampucio

Dom Set 26, 2010 21:36
Cálculo: Limites, Derivadas e Integrais
-
- Limites de sequencias.
por TheoFerraz » Dom Mai 01, 2011 12:49
- 1 Respostas
- 1695 Exibições
- Última mensagem por LuizAquino

Seg Mai 02, 2011 00:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
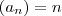
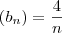

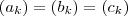 .
.

 não seria
não seria 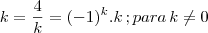




 então
então  , similarmente se faz para o resto.
, similarmente se faz para o resto.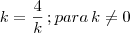
 também servem para a segunda igualdade e desta forma temos como solução os dois,ou seja.
também servem para a segunda igualdade e desta forma temos como solução os dois,ou seja. é natural, então a única resposta válida é
é natural, então a única resposta válida é  .
.

