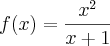
Preciso determinar a imagem. Conheço o método gráfico de fazer isso. Porém o que procuro é o método analítico de se fazer.
Um exemplo de método analítico é a seguinte expressão:
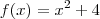
Minha imagem será os reais. Posso utilizar o método da seguinte forma:
Como D=R,
 e
e 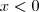 (Para elevar ao quadrado, deve ter sinal de superior >)
(Para elevar ao quadrado, deve ter sinal de superior >)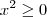 e
e 
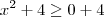 e
e 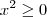 (continua e termina como o do lado esquerdo).
(continua e termina como o do lado esquerdo).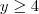
O problema é que já tentei fatorar a primeira função de todas as formas, e não consigo encontrar um jeito de encontrar a imagem dela analiticamente.
Agradeço a ajuda.
Até logo.



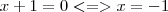
 tem solução.
tem solução.






 , avisa que eu resolvo.
, avisa que eu resolvo.

