 por Aliocha Karamazov » Dom Abr 10, 2011 22:39
por Aliocha Karamazov » Dom Abr 10, 2011 22:39
Olá, pessoal. Resolvi o reguinte exercício na base da tentativa, mas não consigo provar por meio de passos matemáticos.
Calcule a(s) raíz(es) da equação:
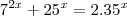
Substituí x por 0 e vi que essa é a única raiz. Mas gostaria de saber como encontrar a reposta através de um método mais rigoroso.
Obrigado desde já!
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por FilipeCaceres » Seg Abr 11, 2011 00:00
por FilipeCaceres » Seg Abr 11, 2011 00:00
Questão
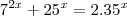
Solução:
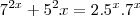
Dividindo tudo por
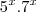
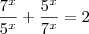
Agora faça o seguinte,
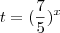
logo
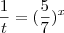
Assim temos,
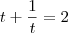
O resto deixo como exercício, qualquer dúvida poste aí.
Abraço
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Aliocha Karamazov » Seg Abr 11, 2011 02:17
por Aliocha Karamazov » Seg Abr 11, 2011 02:17
Muito obrigado, consegui chegar à resposta.
Abraço.
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Provar se é par
por stalone » Seg Dez 21, 2009 23:29
- 5 Respostas
- 3246 Exibições
- Última mensagem por stalone

Seg Dez 13, 2010 13:07
Desafios Difíceis
-
- Provar que ||u|| > 0
por 0 kelvin » Qui Mar 24, 2011 20:35
- 2 Respostas
- 1992 Exibições
- Última mensagem por 0 kelvin

Qui Mar 24, 2011 21:16
Geometria Analítica
-
- Provar
por scggomes » Sex Abr 15, 2011 16:38
- 8 Respostas
- 5976 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 16, 2011 15:56
Cálculo para Funções de Uma Variável Real I
-
- provar que
por anamendes » Ter Jun 19, 2012 07:41
- 1 Respostas
- 1431 Exibições
- Última mensagem por fraol

Qua Jun 20, 2012 21:19
Trigonometria
-
- Provar
por Jovani Souza » Ter Jun 11, 2013 21:03
- 0 Respostas
- 1029 Exibições
- Última mensagem por Jovani Souza

Ter Jun 11, 2013 21:03
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
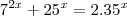

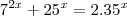

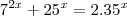
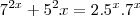
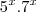
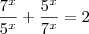
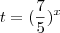
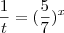
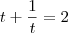




 , avisa que eu resolvo.
, avisa que eu resolvo.

