Resolvendo a desigualdade
 obtemos:
obtemos:Eu tentei fazer da seguinte maneira:
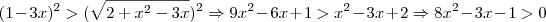
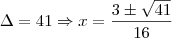
Ainda, pela condição de existência:
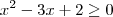
Depois disso, fiz a intersecção com as soluções das duas inequações, mas a resposta saiu diferente do livro. Alguém pode ajudar? Muito obrigado!


 é:
é: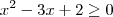 é:
é:
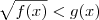
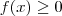 e
e  (i)
(i)![f(x)<[g(x)]^2 f(x)<[g(x)]^2](/latexrender/pictures/3a7485117f703accdf37400e64a36348.png) (ii)
(ii)![0\leq f(x)<[g(x)]^2 0\leq f(x)<[g(x)]^2](/latexrender/pictures/6f065d60587f907c025dfa208f3298f9.png) e
e ![\sqrt{f(x)}<g(x) \Rightarrow 0\leq f(x)<[g(x)]^2 \sqrt{f(x)}<g(x) \Rightarrow 0\leq f(x)<[g(x)]^2](/latexrender/pictures/ac35d35ac3df282a4ae310adeb55d839.png) e
e 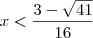

 . Na minha solução, além de
. Na minha solução, além de  .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)