Bom dia estou com muita dificuldades para resolver equações desse tipo:
Se 0<x<pi, as raizes da equação cos^2x - sen ^2( pi - x)=1/2 são:
Obs: o x esta no intervalo o menor igual a x e menor igual a pi.



380625 escreveu:Se, as raízes da equação
são:
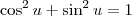 , para qualquer ângulo u. Portanto, a equação é equivalente a:
, para qualquer ângulo u. Portanto, a equação é equivalente a:![\cos^2x - [1 - \cos ^2(\pi - x)]=\frac{1}{2} \cos^2x - [1 - \cos ^2(\pi - x)]=\frac{1}{2}](/latexrender/pictures/79fd8ff8a24b7e161d25a54d5c4bfc88.png)
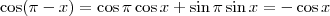 , temos que:
, temos que: ![\cos^2x - [1 - (-\cos x)^2]=\frac{1}{2} \cos^2x - [1 - (-\cos x)^2]=\frac{1}{2}](/latexrender/pictures/6efea19b1c0b8ca487a23805103b4b27.png)
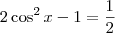
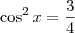
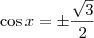
 é
é  . Já o ângulo do segundo quadrante que tem cosseno igual a
. Já o ângulo do segundo quadrante que tem cosseno igual a 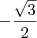 é
é 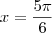 . Portanto, as raízes são
. Portanto, as raízes são 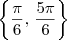
380625 escreveu:estou com muita dificuldades para resolver equações desse tipo
380625 escreveu:Obs: o x esta no intervalo o menor igual a x e menor igual a pi.

Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 .
.
 :
: