gustavoluiss escreveu:Utilizando a definição de módulo, encontre uma expressão equivalente que não possua módulo:
1º :

para x
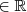
.
Usando a definição de módulo, nós temos que:
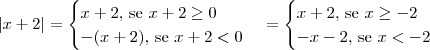
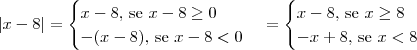
Fazendo um diagrama com os intervalos, nós obtemos a figura abaixo.
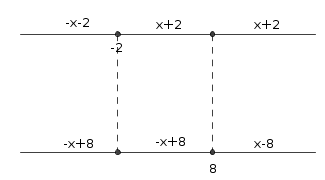
- modulo.png (2 KiB) Exibido 2363 vezes
Sendo assim, nós temos que:
(a) Para x<-2, irá ocorrer (-x-2) + (-x+8) = -2x+6.
(b) Para
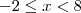
, irá ocorrer (x+2) + (-x+8) = 10.
(b) Para
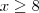
, irá ocorrer (x+2) + (x-8) = 2x-6.
gustavoluiss escreveu:2 º : As sentenças
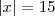
e
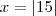
têm o mesmo resultado para qualquer valor real de x? Justifique sua resposta.
Basta você aplicar a definição de módulo e você perceberá que a primeira equação terá duas soluções. Já a segunda terá apenas uma. Tente fazer!
gustavoluiss escreveu:Duas questõezinhas quem puder me explica direito po eu ficarei muito grato estará contribuindo para um país melhor no futuro.
Esperamos que sim. Só o tempo dirá se essa geração de pessoas que se formaram obtendo ajuda aqui do fórum (uma ajuda voluntária, vale destacar) também farão suas contribuições (voluntárias) em causas sociais.
 para x E R
para x E R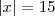 e
e 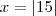 têm o mesmo resultado para qualquer valor real de x? Justifique sua resposta.
têm o mesmo resultado para qualquer valor real de x? Justifique sua resposta.

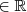 .
.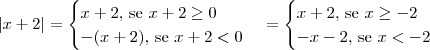
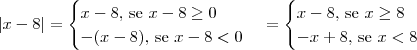
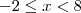 , irá ocorrer (x+2) + (-x+8) = 10.
, irá ocorrer (x+2) + (-x+8) = 10.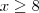 , irá ocorrer (x+2) + (x-8) = 2x-6.
, irá ocorrer (x+2) + (x-8) = 2x-6.

 .
.
 :
: