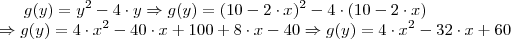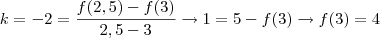Seguinte, a questão nada mais é do que descobrir o coeficiente angular da reta e levantar a equação do gráfico nos intervalos dados, vamos ver se consigo explicar.
Primeiramente, o enunciado nos diz que a função é cíclica com um período de 10, isto é, ela repete seus valores a cada 10 "passadas", então se ele deseja descobrir o valor de
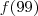
basta-nos achar o valor de

pois 99 irá se repetir 9 vezes e terminar no valor 9 (pois 99 dividido por 10 dá 9 com resto 9). Sabendo disso, iremos calcular o valor de

, o que não é complicado, veja:
O valor

está entre 7,5 (cheguei a esse valor verificando que ele está exatamente na metade do intervalo 5 e 10, logo
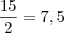
) e 10, os quais possuem as respectivas imagens

e

, logo o que temos que fazer inicialmente é achar o coeficiente angular da reta, faremos isso dividindo a diferença entre as imagens pela diferença entre as coordenadas, conforme abaixo:
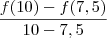
Logo, temos o valor do coeficiente angular daquela reta, vamos chamá-lo de

para facilitar. Agora vamos achar o valor de

, iremos fazer exatamente a mesma coisa, só que já sabemos que o coeficiente angular tem que ser igual a 2 (calculado anteriormente), então temos:
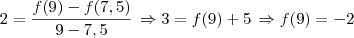
Sabendo disso, temos que

.
A letra b, pode ser feita de maneira bem parecida, primeiro acharemos o coeficiente angular da reta que está no intervalo 2,5 e 5, que chamaremos de k.
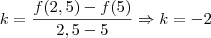
Utilizando do mesmo raciocínio, igualemos o coeficiente angular da reta a divisão entre a diferença de
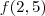
e
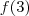
e a diferença entre 2,5 e 3, conforme abaixo:

Logo:
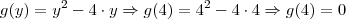
Para acharmos a equação de
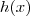
no intervalo
![[2.5,5] [2.5,5]](/latexrender/pictures/c53057b6c9a3009e1c833f96ff8ce4da.png)
temos que levantar a equação da reta entre os intervalos solicitados, já sabemos que o coeficiente angular é -2, então a equação da reta fica:
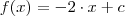
Para acharmos o valor de

, devemos igualar

a zero, isso ocorre quando

, logo:

Então temos:
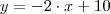
Aplicando essa função na composta

teremos:
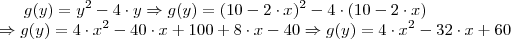
no intervalo
![[2.5,5] [2.5,5]](/latexrender/pictures/c53057b6c9a3009e1c833f96ff8ce4da.png)
Espero ter ajudado, qualquer dúvida, por favor poste.
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
 seja uma função ímpar (isto é, f(-x) = -f(x) e periódica, com período 10 (isto é f(x) = f(x+10)). O gráfico da função no intervalo [0,5] é apresentado abaixo.
seja uma função ímpar (isto é, f(-x) = -f(x) e periódica, com período 10 (isto é f(x) = f(x+10)). O gráfico da função no intervalo [0,5] é apresentado abaixo.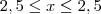


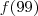 basta-nos achar o valor de
basta-nos achar o valor de  pois 99 irá se repetir 9 vezes e terminar no valor 9 (pois 99 dividido por 10 dá 9 com resto 9). Sabendo disso, iremos calcular o valor de
pois 99 irá se repetir 9 vezes e terminar no valor 9 (pois 99 dividido por 10 dá 9 com resto 9). Sabendo disso, iremos calcular o valor de  está entre 7,5 (cheguei a esse valor verificando que ele está exatamente na metade do intervalo 5 e 10, logo
está entre 7,5 (cheguei a esse valor verificando que ele está exatamente na metade do intervalo 5 e 10, logo 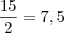 ) e 10, os quais possuem as respectivas imagens
) e 10, os quais possuem as respectivas imagens  e
e  , logo o que temos que fazer inicialmente é achar o coeficiente angular da reta, faremos isso dividindo a diferença entre as imagens pela diferença entre as coordenadas, conforme abaixo:
, logo o que temos que fazer inicialmente é achar o coeficiente angular da reta, faremos isso dividindo a diferença entre as imagens pela diferença entre as coordenadas, conforme abaixo:
 para facilitar. Agora vamos achar o valor de
para facilitar. Agora vamos achar o valor de 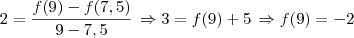
 .
.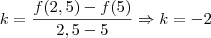
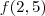 e
e 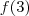 e a diferença entre 2,5 e 3, conforme abaixo:
e a diferença entre 2,5 e 3, conforme abaixo:
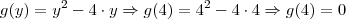
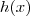 no intervalo
no intervalo ![[2.5,5] [2.5,5]](/latexrender/pictures/c53057b6c9a3009e1c833f96ff8ce4da.png) temos que levantar a equação da reta entre os intervalos solicitados, já sabemos que o coeficiente angular é -2, então a equação da reta fica:
temos que levantar a equação da reta entre os intervalos solicitados, já sabemos que o coeficiente angular é -2, então a equação da reta fica: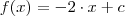
 , devemos igualar
, devemos igualar  a zero, isso ocorre quando
a zero, isso ocorre quando  , logo:
, logo:
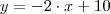
 teremos:
teremos: