Estou com problemas na resolução de exercicios sobre função composta... sei que para calcular uma fog(x) por exemplo devemos sustituir o x da f(x) pelo valor da f(g) ... mas... ainda tenho muitas dúvidas...
A questão é:
Se f (x) = x² - 2 e g (x) = 5x +
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) , dê o domínio das funções e ache:
, dê o domínio das funções e ache:a) f o f (x)
b) g o g (x)
c) f o g (x)
d) g o f (x)
Eu estou resolvendo assim... Porém não sei se está correto.... Caso esteja errado me corrijam, por favor...
a) f o f (x)
= f (f (x))
(?2– 2)² - 2
?4 - 4 ?2 + 4 – 2
?4 - 4 ?2 + 2
b) g o g (x)
= g (g(x))
5 . (5 ? +
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) ) +
) + ![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
25 ? + 5
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) +
+ ![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
25 ? + 6
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
c) f o g (x)
= f (g (x))
5 . (5 ? +
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) )² - 2
)² - 225 ? ² + 10 ?
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) + ? - 2
+ ? - 225 ?² + 10 ? . ?1/2 + ? - 2
25 ?² + 10?3/2 + ? – 2
d) g o f (x)
= g (f (x))
5 . (?2– 2) +
![\sqrt[]{x^2-2} \sqrt[]{x^2-2}](/latexrender/pictures/edebf682d9dc1acefbbf1f490e7a913b.png)
5 ?² - 10 + (?2– 2)1/2
Obs: não consegui resolver esse calculo...
Agora a maior dúvida...
Como encontrar o dominio???
Me ajudem. por favor!!!



 . O
. O  (domínio) não pode ser qualquer número, pois dentro da raiz só é possível valor
(domínio) não pode ser qualquer número, pois dentro da raiz só é possível valor 
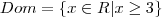



 .
.
 :
: