Um casal de namorados marca um encontro numa ciclovia;ele vem do norte e ela do sul. O rapaz pedala a uma velocidade de 32 km/h e a moça pedala a 24 km/h. No instante em que a distancia entre eles é de 28 km, uma abelha, que voa a 20 km/h, parte de um ponto entre os dois até encontrar um deles; então ela volta em direção ao outro e continua nesse vaivém até morrer prensada pelas rodas das bicicletas no momento em que o casal se encontra. Quantos quilômetros voou a abelha?
gente em não sei nem por onde começar, o livro até tem a resposta, mas eu não consigo resolver a questão. Alguem pode me ajudar ?
Obrigado.





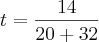
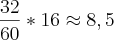
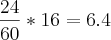
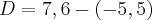

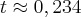


 .
.



