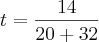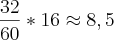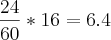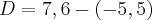por luishennrique » Qui Dez 30, 2010 20:15
por luishennrique » Qui Dez 30, 2010 20:15
Bom gente preciso de uma ajudinha com este problema.
Um casal de namorados marca um encontro numa ciclovia;ele vem do norte e ela do sul. O rapaz pedala a uma velocidade de
32 km/h e a moça pedala a
24 km/h. No instante em que a distancia entre eles é de
28 km, uma abelha, que voa a
20 km/h, parte de um ponto entre os dois até encontrar um deles; então ela volta em direção ao outro e continua nesse vaivém até morrer prensada pelas rodas das bicicletas no momento em que o casal se encontra. Quantos quilômetros voou a abelha?
gente em não sei nem por onde começar, o livro até tem a resposta, mas eu não consigo resolver a questão. Alguem pode me ajudar ?
Obrigado.

-
luishennrique
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Dez 30, 2010 19:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Elcioschin » Sex Dez 31, 2010 15:14
por Elcioschin » Sex Dez 31, 2010 15:14
Tempo para os dois se encontrarem:
D = (V + v)*t ------> 28 = (32 + 24)*t ----> 28 = 56*t ----> t = 0,5 h (ou 30 min)
Este tempo é o mesmo em que a abelha voou -----> d = v'*t ----> d = 20*0,5 ----> d = 10 km
Coitada da abelha: deve ter morrido extenuada
Coitado também do casal de namorados: como as rodas bateram de frente numa velocidade equivalente a 56 km/h o tombo de ambos dever sido bem feio.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por luishennrique » Sáb Jan 01, 2011 19:06
por luishennrique » Sáb Jan 01, 2011 19:06
Elcioschin escreveu:Tempo para os dois se encontrarem:
D = (V + v)*t ------> 28 = (32 + 24)*t ----> 28 = 56*t ----> t = 0,5 h (ou 30 min)
Este tempo é o mesmo em que a abelha voou -----> d = v'*t ----> d = 20*0,5 ----> d = 10 km
Coitada da abelha: deve ter morrido extenuada
Coitado também do casal de namorados: como as rodas bateram de frente numa velocidade equivalente a 56 km/h o tombo de ambos dever sido bem feio.
Muito Obrigado
Elcioschin.
-
luishennrique
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Dez 30, 2010 19:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por PedroSantos » Dom Jan 02, 2011 07:52
por PedroSantos » Dom Jan 02, 2011 07:52
Fiquei com dúvidas em relação à proposta de resolução apresentada pelo Elcioschin. Por isso recorri-me do metodo experimental
Inicialmente a abelha parte de um ponto intermédio entre o rapaz e a rapariga. Por isso apliquei a expressão

para
a igual à velocidade da abelha e
b para a velocidade de um dos outros.Seja
b a velocidade do rapaz.
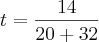
O que resulta em aproximadamente 16 min.
Imaginemos que o rapaz, e a rapariga se posicionam na reta real. Onde, inicialmente, o rapaz ocupa o ponto de abscissa -14 e a rapariga a abscissa 14. Após este primeiro momento de 16 min o rapaz percorreu:
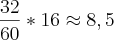
e ocupa agora a abscissa -5,5.
A rapariga percorreu
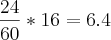
e ocupa a abscissa 7,6.
Agora, e até ao final, utilizo as velocidades do rapaz e da rapariga.
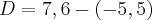

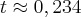
Ou seja
t=14 min
Assim a abelha percorreu um total de (14min+16min)*20km/h. Provavelmente a primeira parte da minha demonstração é indeferente para a resolução do problema.
-
PedroSantos
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Dez 01, 2010 16:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ensino secundário
- Andamento: cursando
 por luishennrique » Dom Jan 02, 2011 23:00
por luishennrique » Dom Jan 02, 2011 23:00
PedroSantos escreveu:Fiquei com dúvidas em relação à proposta de resolução apresentada pelo Elcioschin. Por isso recorri-me do metodo experimental
Inicialmente a abelha parte de um ponto intermédio entre o rapaz e a rapariga. Por isso apliquei a expressão

para
a igual à velocidade da abelha e
b para a velocidade de um dos outros.Seja
b a velocidade do rapaz.
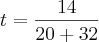
O que resulta em aproximadamente 16 min.
Imaginemos que o rapaz, e a rapariga se posicionam na reta real. Onde, inicialmente, o rapaz ocupa o ponto de abscissa -14 e a rapariga a abscissa 14. Após este primeiro momento de 16 min o rapaz percorreu:
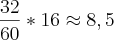
e ocupa agora a abscissa -5,5.
A rapariga percorreu
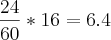
e ocupa a abscissa 7,6.
Agora, e até ao final, utilizo as velocidades do rapaz e da rapariga.
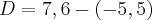

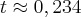
Ou seja
t=14 min
Assim a abelha percorreu um total de (14min+16min)*20km/h. Provavelmente a primeira parte da minha demonstração é indeferente para a resolução do problema.
Me parece complicado, mas de qualquer forma valeu ?

-
luishennrique
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Dez 30, 2010 19:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- filhos do casal
por maria cleide » Dom Mai 22, 2011 20:25
- 1 Respostas
- 1246 Exibições
- Última mensagem por norberto

Dom Mai 22, 2011 22:15
Sequências
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10718 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9730 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
-
- Problema..
por ANDRE RENATO PROFETA » Sex Mar 13, 2009 00:36
- 1 Respostas
- 3315 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 14:58
Álgebra Elementar
-
- Problema
por ginrj » Qua Jun 03, 2009 19:19
- 3 Respostas
- 4612 Exibições
- Última mensagem por Cleyson007

Dom Jun 07, 2009 11:48
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.