Demonstrar que a soma dos n primeiros números naturais é igual a
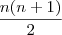 .
. Resolução
Indiquemos por
 a soma procurada
a soma procurada  = 1+2+3+...n
= 1+2+3+...n1º) Para n = 1 a hipótese é válida porque
 = 1 =
= 1 = 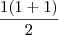
2º) Suponhamos que
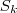 = 1+2+3+...+ k =
= 1+2+3+...+ k = 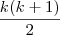
Demonstraremos que
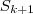 = 1+2+3+...+k+(k+1) =
= 1+2+3+...+k+(k+1) = 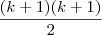
De fato:
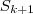 =
= 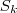 +
+  =
= 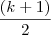 + (k+1) =
+ (k+1) = 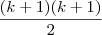 .
.Bom, sei que para provar por indução ele tem que provar que a hipótese é válida para n =1 e para n+1
 0 (me corrijam se eu estiver errado) . Esse exercício me deixou um pouco confuso. n igual a 1 quer dizer que o último termo da sequência é 1? Ou a soma de todos os termos é igual a 1? Ou que a sequência tem apenas 1 termo?
0 (me corrijam se eu estiver errado) . Esse exercício me deixou um pouco confuso. n igual a 1 quer dizer que o último termo da sequência é 1? Ou a soma de todos os termos é igual a 1? Ou que a sequência tem apenas 1 termo? Esta parte não faz sentido para mim.
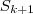 =
= 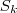 +
+  =
= 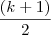 + (k+1) =
+ (k+1) = 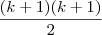 .
.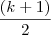 + (k+1) =
+ (k+1) = 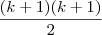 . Essa igualdade é falsa ou eu que entendi errado? Grato desde já !
. Essa igualdade é falsa ou eu que entendi errado? Grato desde já !

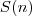 é uma função da variável discreta
é uma função da variável discreta  tal que
tal que 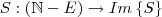 , onde
, onde  é um possível conjunto exclusão pertinente, e verificamos que o natural
é um possível conjunto exclusão pertinente, e verificamos que o natural 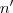 ,de fato, satisfaz a função então é verdade que
,de fato, satisfaz a função então é verdade que  também a satisfaz, se
também a satisfaz, se 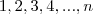 é dada por
é dada por 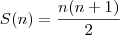 . De fato, para n=3, por exemplo, ela é satisfeita.
. De fato, para n=3, por exemplo, ela é satisfeita.
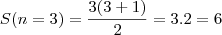
 . Logo, é interessante mostrar q ela é válida para
. Logo, é interessante mostrar q ela é válida para  e depois para
e depois para  .
.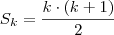 , a hipótese de indução, então
, a hipótese de indução, então 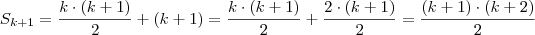 que é a tese da indução.
que é a tese da indução. sendo que
sendo que 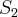 = 2 quando eu substituo em
= 2 quando eu substituo em 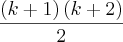 eu não encontro
eu não encontro  .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
