 por Danilo » Dom Abr 22, 2012 03:41
por Danilo » Dom Abr 22, 2012 03:41
Estava resolvendo um exercicio que pedia para estudar o sinal da expressão ax+b para a < 0 e fiquei com uma dúvida.
fiz assim: para ax+b > 0 (a < 0) x < b/a a dúvida é porque na resposta está -b/a e nao b/a já que a é negativo e b aparece no primeiro lado da desigualdade negativo também.. obrigado.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por DanielFerreira » Dom Abr 22, 2012 13:46
por DanielFerreira » Dom Abr 22, 2012 13:46
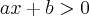
Sabemos que:
a < 0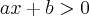


Como
a < 0, então a divisão
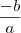
é positiva.
Não entendi sua dúvida!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Danilo » Dom Abr 22, 2012 13:52
por Danilo » Dom Abr 22, 2012 13:52
Então, temos a expressão ax+b
vamos supor que a seja negativo. queremos valores de x para os quais a expressão é positiva, então queremos ax+b > 0
ax + b >0
somando a ambos os membros - b temos:
ax > -b multiplicando a ambos os membros por - 1 temos:
ax < b
x< b/a
na resposta do livro está -b/a e não b/a. Só querendo entender o porquê de ser -b/a.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por DanielFerreira » Dom Abr 22, 2012 14:02
por DanielFerreira » Dom Abr 22, 2012 14:02
Danilo escreveu:Então, temos a expressão ax+b
vamos supor que a seja negativo. queremos valores de x para os quais a expressão é positiva, então queremos ax+b > 0
ax + b >0
somando a ambos os membros - b temos:
ax > -b multiplicando a ambos os membros por - 1 temos:
- ax < b
x< - b/a
na resposta do livro está -b/a e não b/a. Só querendo entender o porquê de ser -b/a.
Esqueceu de trocar o sinal!!
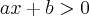


"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Danilo » Dom Abr 22, 2012 23:42
por Danilo » Dom Abr 22, 2012 23:42
Compreendi! /o\
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por DanielFerreira » Ter Abr 24, 2012 20:20
por DanielFerreira » Ter Abr 24, 2012 20:20
vlw.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Qual é o sinal da expressão abaixo?
por andersontricordiano » Sex Ago 12, 2011 22:26
- 3 Respostas
- 4574 Exibições
- Última mensagem por andersontricordiano

Seg Ago 15, 2011 20:29
Trigonometria
-
- [Duvida] Potenciação [Sinal]
por MiyaChan » Qua Jun 01, 2016 19:15
- 3 Respostas
- 4257 Exibições
- Última mensagem por Cleyson007

Dom Jun 05, 2016 11:02
Sequências
-
- [Dúvida ANOVA] Uma dúvida sobre a estatística correta
por gustamfar » Ter Mai 22, 2018 18:19
- 0 Respostas
- 11054 Exibições
- Última mensagem por gustamfar

Ter Mai 22, 2018 18:19
Estatística
-
- Duvida em expressão
por ginrj » Sex Mar 06, 2009 18:45
- 2 Respostas
- 4222 Exibições
- Última mensagem por ginrj

Sáb Mar 07, 2009 12:01
Álgebra Elementar
-
- Expressão duvida !!!
por LuizCarlos » Qui Ago 11, 2011 14:57
- 1 Respostas
- 1641 Exibições
- Última mensagem por Molina

Qui Ago 11, 2011 16:40
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


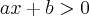


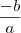 é positiva.
é positiva.