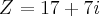por lieberth » Qua Jun 10, 2009 20:51
por lieberth » Qua Jun 10, 2009 20:51
estou com dúvida no i
z = (x,y)

=-1
i=(0,1)
então....(0,1)(0,1) = (0-1,0+0) = (-1,0)
z = (x=-1,y=0) = (-1,0)
onde x é a parte real de z e y a parte imaginária de z
está certo?
então o

=x eu posso dizer de acordo com isso que

ou -1 é a parte real de z?
OBRIGADO
-
lieberth
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Jun 09, 2009 14:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Marcampucio » Qua Jun 10, 2009 21:54
por Marcampucio » Qua Jun 10, 2009 21:54
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por lieberth » Sex Jun 12, 2009 18:04
por lieberth » Sex Jun 12, 2009 18:04
mas pode mudar as letras? ex: a+bi
poderia ser x+yi?
A=X E B=Y
o i no meu livro está i= (0,1) esse i é o mesmo que
![\sqrt[]{-1} \sqrt[]{-1}](/latexrender/pictures/96dee42b6f915f610697937e8c654c44.png)
-
lieberth
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Jun 09, 2009 14:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por lieberth » Sex Jun 12, 2009 19:52
por lieberth » Sex Jun 12, 2009 19:52
lieberth escreveu:mas pode mudar as letras? ex: a+bi
poderia ser x+yi?
A=X E B=Y
o i no meu livro está i= (0,1) esse i é o mesmo que
![\sqrt[]{-1} \sqrt[]{-1}](/latexrender/pictures/96dee42b6f915f610697937e8c654c44.png)
-
lieberth
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Jun 09, 2009 14:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por lieberth » Sex Jun 12, 2009 20:01
por lieberth » Sex Jun 12, 2009 20:01
olha essa:

certo essa?
-
lieberth
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Jun 09, 2009 14:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Sex Jun 12, 2009 20:10
por Cleyson007 » Sex Jun 12, 2009 20:10
Olá Lieberth!
Segue resolução:
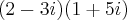

-->
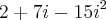
--> Lembrando que

Portanto:
 --> Logo o número complexo procurado é:
--> Logo o número complexo procurado é: 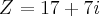

Sua resposta está correta.
Lieberth, por favor abra um novo tópico para cada dúvida, ok?Um abraço.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Molina » Sex Jun 12, 2009 20:18
por Molina » Sex Jun 12, 2009 20:18
lieberth escreveu:olha essa:

certo essa?
Correto.
A substituição é esta mesma.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- unidade imaginaria
por lieberth » Ter Jun 16, 2009 17:24
- 2 Respostas
- 1850 Exibições
- Última mensagem por Cleyson007

Qua Jun 17, 2009 10:37
Números Complexos
-
- [parte real e imaginária de complexos] ajuda em uma questão
por caroline1303 » Seg Out 08, 2012 01:15
- 1 Respostas
- 1931 Exibições
- Última mensagem por young_jedi

Seg Out 08, 2012 10:18
Números Complexos
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17104 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
-
- Numeros complexos!
por Estela » Seg Mar 17, 2008 00:57
- 7 Respostas
- 13313 Exibições
- Última mensagem por andegledson

Seg Nov 02, 2009 21:41
Números Complexos
-
- Números Complexos
por michelle » Dom Ago 31, 2008 15:35
- 3 Respostas
- 10312 Exibições
- Última mensagem por admin

Dom Ago 31, 2008 21:00
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 =-1
=-1 =x eu posso dizer de acordo com isso que
=x eu posso dizer de acordo com isso que  ou -1 é a parte real de z?
ou -1 é a parte real de z?
 =-1
=-1 =x eu posso dizer de acordo com isso que
=x eu posso dizer de acordo com isso que  ou -1 é a parte real de z?
ou -1 é a parte real de z?

![\sqrt[]{-1} \sqrt[]{-1}](/latexrender/pictures/96dee42b6f915f610697937e8c654c44.png)




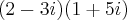
 -->
--> 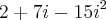 --> Lembrando que
--> Lembrando que