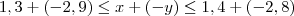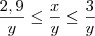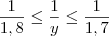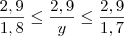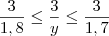por Danilo » Sáb Mar 17, 2012 23:53
por Danilo » Sáb Mar 17, 2012 23:53
Pessoal, estou postando esses exercício aqui porque tenho que entregá-los segunda feira, e estous tentando ao máximo resolver sozinho, mas alguns que está difícil chegar a um resultado em tempo hábil. Fiquei o dia todo estudando sobre os números reais e as ''regras'' que devemos seguir nas desigualdades no livro calculo a uma variavel . Enfim, vamos ao exercício. Preciso mostrar que 2 proposições são verdadeiras.
São elas:
(a) Se 1,3 ? x ? 1,4 e 2,8 ? y ? 2,9 , então - 1,6 ? x - y ? - 1,4.
(b) Se 2,9 ? x ? 3 e 1,7 ? y ? 1,8 , então 2,9/1,8 ? x/y ? 3/1,7
Sei que para provar que uma proposição é falta basta exibir um contra exemplo, ou que a hipótese e a tese devem ser igualmente satisfeitas. Mas não sei como aplicar nessas inequações. Se alguem puder dar um caminho, agradeço. Enquanto isso vou tentando aqui... obrigado aeww
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Dom Mar 18, 2012 01:15
por LuizAquino » Dom Mar 18, 2012 01:15
Danilo escreveu:(a) Se 1,3 ? x ? 1,4 e 2,8 ? y ? 2,9 , então - 1,6 ? x - y ? - 1,4.
Se

, então

. Ou ainda, podemos escrever que
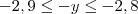
.
Somando membro a membro essa última inequação com a inequação
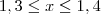
, temos que:
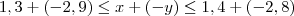

Danilo escreveu:(b) Se 2,9 ? x ? 3 e 1,7 ? y ? 1,8 , então 2,9/1,8 ? x/y ? 3/1,7
Como y é positivo (e não nulo), podemos dizer que:
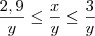
Além disso, também podemos dizer que:
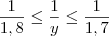
Multiplicando essa inequação por 2,9 e por 3, obtemos que:
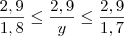
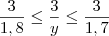
Sendo assim, temos que:

Temos então que:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Danilo » Dom Mar 18, 2012 01:49
por Danilo » Dom Mar 18, 2012 01:49
Obrigado professor!!!!!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Nao consigo mostrar
por 380625 » Sáb Jun 02, 2012 16:42
- 1 Respostas
- 1147 Exibições
- Última mensagem por Russman

Sáb Jun 02, 2012 17:52
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]Mostrar uma expressão.
por amigao » Dom Mai 26, 2013 21:28
- 1 Respostas
- 1071 Exibições
- Última mensagem por e8group

Dom Mai 26, 2013 22:02
Cálculo: Limites, Derivadas e Integrais
-
- Mostrar que é Subespaço Vetorial
por Razoli » Sex Set 26, 2014 22:03
- 3 Respostas
- 1921 Exibições
- Última mensagem por adauto martins

Seg Set 29, 2014 12:33
Álgebra Linear
-
- Derivadas Parciais - Mostrar que:
por Cleyson007 » Ter Nov 04, 2014 16:20
- 1 Respostas
- 1049 Exibições
- Última mensagem por Russman

Ter Nov 04, 2014 22:19
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] Como mostrar esse lim?
por jandercw » Seg Set 19, 2011 17:17
- 1 Respostas
- 1509 Exibições
- Última mensagem por MarceloFantini

Seg Set 19, 2011 17:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , então
, então  . Ou ainda, podemos escrever que
. Ou ainda, podemos escrever que 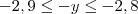 .
.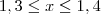 , temos que:
, temos que: