


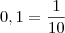 . Para marcar o segmento, basta pegar uma régua, colocar no papel e riscar 10cm, mesma coisa para o de 20cm.
. Para marcar o segmento, basta pegar uma régua, colocar no papel e riscar 10cm, mesma coisa para o de 20cm. . Tomando agora a segunda casa decimal, fica
. Tomando agora a segunda casa decimal, fica 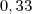 e
e  . O número irracional será
. O número irracional será 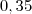 . Isto mostra que ele é maior que o primeiro e menor que o segundo. Matematicamente, expressamos isso como
. Isto mostra que ele é maior que o primeiro e menor que o segundo. Matematicamente, expressamos isso como  . Daí, o ponto irracional ficará ENTRE os pontos racionais citados.
. Daí, o ponto irracional ficará ENTRE os pontos racionais citados.


 .
. , nós já sabemos só de olhar pra ele que ele não é um número irracional.
, nós já sabemos só de olhar pra ele que ele não é um número irracional. ![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) , que é lido como raíz quadrada de dois. Digita ele em qualquer calculadora e aperta o símbolo =. A calculadora vai exibir quanto vale esse número.
, que é lido como raíz quadrada de dois. Digita ele em qualquer calculadora e aperta o símbolo =. A calculadora vai exibir quanto vale esse número.![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) na calculadora e aperta igual, você obtém 1,41421356 note que preencherá todas casas da calculadora.
na calculadora e aperta igual, você obtém 1,41421356 note que preencherá todas casas da calculadora.![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)

nietzsche escreveu:Luiz Carlos,
um número se chama racional quando ele pode ser escrito como uma fração. O nome racional é uma derivação de razão, isto é, a razão entre dois números. Razão é aquela idéia de uma sobre o outro. Por exemplo, se quiser escrever matematicamente a razão entre 2 e 3, nós escrevemos:
Então se você falar em fração, razão, um sobre o outro, etc... você já tem que pensar num número escrito em fração, por exemplo,.
Agora os número irracionais são aqueles que não podem ser escritos como a razão de dois números. Então se considerarmos novamente a razão entre 2 e 3, isto é, o número escrito como, nós já sabemos só de olhar pra ele que ele não é um número irracional.
Agora pense no número, que é lido como raíz quadrada de dois. Digita ele em qualquer calculadora e aperta o símbolo =. A calculadora vai exibir quanto vale esse número.
Agora você deve lembra que a fração 2/3 é o mesmo que nós calcularmos 2 dividido por 3. Se você digitar isso na calculadora e apertar o = vai obter 0,66666666666.
Se você digitar 5/4 na calculadora e apertar o igual você obtém 1,25.
Se você digitarna calculadora e aperta igual, você obtém 1,41421356 note que preencherá todas casas da calculadora.
A diferença entre a raiz quadrada de 2 e o 2/3 é que no 2/3 percebemos a ordem lógica dos números que vem depois da vírgula. Na realidade o 0,666666666666666666666666666 vai com 6666 um monte de vezes, mas a calculador não tem que parar. Ás vezes ela arredonda colocando um 7 na última casa.
Enfim, o número racional tem uma "ordem" nos seus dígitos quando está escrito na forma decimal. Forma decimal é o número com vírgula, como esse 1,25. Agora o irracional não tem como saber a ordem. Tem calculadoras que calculam até mil casas após a vírgula e o pior é que não se sabe o padrão dos números que se repete. O 0,66666 já se sabe que vira sempre um 6, mesmo que tenha infinitos 6 depois da vírgula. Agora os números irracionais, não tem como sabe. Você pode também pensar no irracional usado como adjetivo do português. É irracional porque não tem lógica, é meio louco, não tem como se saber o que vira.
Tendo uma noção do que é um número racional e um irracional e como ajuda de uma calculadora, você pode escrever esses números numa reta. Você escreve aproximadamente. Por exemplo, vou escrever esses números que falei numa reta real. Lembre-se que os números reais são os mais conhecidos, e ele pode ser representado por uma reta, que é comum se chamar reta real.
Reta real :
2/3 5/4
___________________x____________x_______________x____________________ >>>
Essas setas indicam que pra direita os números crescem. A reta tem infinitos pontos. Cada ponto é um número. Onde eu coloquei x é porque estão os pontos que eu queria achar na reta. Em cima do x eu coloco o valor dos pontos. Basicamente achar os pontos na retá é dizer mais menos onde eles estão. Você poderia achar pensando na reta como uma régua. Aí para o número 2/3 , você iria ter que fazer um x na régua onde vale 0,66666. E assim por diante.
Pode parecer meio complicado mas esse conceito de número irracional, racional, real é mais complicado de se entender no ensino médio porque você precisa associar com a reta, com alguma coisa geométrica, senão parece que não faz sentido. Número irracional até hoje é misterioso.
Para ver mais sobre o assunto veja no wikipedia:
http://pt.wikipedia.org/wiki/N%C3%BAmero_racional


Juvenal escreveu:Mas a pergunta é: Como localizo uma dízima periódica na reta, por exemplo: 0,333333333... 0,373737373737....
Como demonstrar na reta a dízima 0,333...
 , mas agora não sei como representar essa fração!
, mas agora não sei como representar essa fração!
LuizCarlos escreveu:Percebi que número racional não precisa realmente aproximar! entendi o que o amigo LuizAquino explicou.

LuizAquino escreveu:LuizCarlos escreveu:Percebi que número racional não precisa realmente aproximar! entendi o que o amigo LuizAquino explicou.
Prezado Luiz Carlos, você está fazendo confusão.
Eu não expliquei coisa alguma nesse seu tópico.
Quem lhe explicou isso foi o colega MarceloFantini. É a ele que você deve agradecer. Assim como ao nietzsche e ao Juvenal, que também lhe ajudaram a responder a sua dúvida.

 um pouco depois do 0,333... =
um pouco depois do 0,333... =  e entre eles põe o número irracional 0,35335333533335... em forma de dízima mesmo.
e entre eles põe o número irracional 0,35335333533335... em forma de dízima mesmo.
Juvenal escreveu:Coloca o 0,37373737... =um pouco depois do 0,333... =
e entre eles põe o número irracional 0,35335333533335... em forma de dízima mesmo.
 é uma fração própria, então significa que é menor que 1, então fica entre 0 e 1, dividindo a unidade em 3 partes iguais, pego a primeira e lá estará localizado
é uma fração própria, então significa que é menor que 1, então fica entre 0 e 1, dividindo a unidade em 3 partes iguais, pego a primeira e lá estará localizado  . Agora acompanhe meu raciocínio, 0,37373737.... =
. Agora acompanhe meu raciocínio, 0,37373737.... =  , então teria que dividir a unidade em 99 partes iguais e pegar 37, mas não tem como fazer isso, seria muito trabalhoso e sem necessidade, então qual a forma para representar essa fração na reta numérica. Porque você somente falou, coloca um pouco depois de 0,333...., então essa sua explicação da a entender que tenho que deduzir onde ficará a marcação de
, então teria que dividir a unidade em 99 partes iguais e pegar 37, mas não tem como fazer isso, seria muito trabalhoso e sem necessidade, então qual a forma para representar essa fração na reta numérica. Porque você somente falou, coloca um pouco depois de 0,333...., então essa sua explicação da a entender que tenho que deduzir onde ficará a marcação de  , ou nesse caso de frações com denominadores muito altos, não tem uma marcação precisa na reta. No aguardo.
, ou nesse caso de frações com denominadores muito altos, não tem uma marcação precisa na reta. No aguardo.

Juvenal escreveu:Sim, como um professor demonstraria isso numa lousa.


Juvenal escreveu:Não entendi o final do que vc quis dizer.
Devo lembrar que o conjunto dos números racionais unido com o conjunto dos números Irracionais forma o conjunto dos números reais.
Logo numa reta real você tem qualquer número racional quanto tem qualquer número Irracional.


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

