O resultado da simplificação da expressão 7^9+4X7^6+5X7^3+2/344² é
a) 7³ + 2
b)7³ - 4
c)7³ + 5
d) 3
e) 1
Já tentei várias vezes naum sei se tem alguma coisa errada na questão ou algum passo q ainda naum visualizei. Ajudem!!!



Pri Ferreira escreveu:O resultado da simplificação da expressão 7^9+4X7^6+5X7^3+2/344² é
a) 7³ + 2
b)7³ - 4
c)7³ + 5
d) 3
e) 1
Pri Ferreira escreveu:Já tentei várias vezes naum sei se tem alguma coisa errada na questão ou algum passo q ainda naum visualizei.
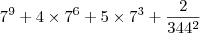

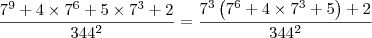
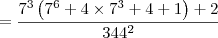
![= \dfrac{7^3\left[ (7^3 + 2)^2 + 1\right] + 2}{344^2} = \dfrac{7^3\left[ (7^3 + 2)^2 + 1\right] + 2}{344^2}](/latexrender/pictures/e3321cc1381e1676b6c4602f7b791595.png)

![= \dfrac{\left(7^3 + 2\right)\left[7^3\left(7^3 + 2\right) + 1\right]}{344^2} = \dfrac{\left(7^3 + 2\right)\left[7^3\left(7^3 + 2\right) + 1\right]}{344^2}](/latexrender/pictures/3e6162b472d180bb38edf3e0c11deb7e.png)
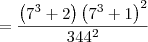



Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.