Pjrleal escreveu:Oi, preciso que alguém resolva e explique o problema que colocarei abaixo, pois faço direito e sou mto ruim em matematica.
É mais uma questão de interpretação de texto do que de Matemática.
Pjrleal escreveu:Para servir suco a algumas crianças, foram compradas duas garrafas de suco de uva com 1,5 cada uma.
Eu presumo que cada garrafa tenha 1,5 L, apesar de você não ter escrito o "L". Temos então 3 L de suco.
Pjrleal escreveu:Como o suco era concentrado, foi feita uma diluição em água na seguinte proporção: 5 partes de suco para 3 partes de água.
Ou seja, considerando o total da mistura (isto é, o suco mais a água), se dividimos em 8 partes iguais, então 5 delas serão de suco e 3 delas serão de água.
Suponha que o total da mistura seja
x litros. Temos então que:

Isso porque haviam 3 L de suco.
Resolvendo essa equação, obtemos que

.
Portanto, o total da mistura é
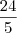
L.
Pjrleal escreveu:Depois de diluído, todo o suco foi servido em copos de 200ml cada um. O número máximo de copos que puderam ser servidos foi?
Sabemos que 1 L equivale a 1.000 ml. Sendo assim, temos que
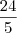
L equivale a 4.800 ml.
A partir disso, fica fácil saber quantos copos no máximo poderão ser servidos.



 .
.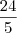 L.
L.

 .
.



