nathyn escreveu:1)
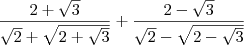
nathyn escreveu:Eu multipliquei cada fração pelo inverso do seu denominador, para eliminar as raizes do mesmo e ficou:
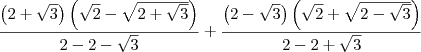
Como o denominador da primeira era
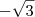
, o sinal do numerador da primeira foram mudados, ficando:
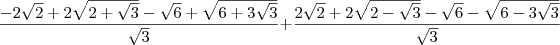
Calculando...
![\frac{2\sqrt{2 + \sqrt{3}} - 2\sqrt{6} + \sqrt{6 + 3\sqrt{3}} - \sqrt[]{6 - 3\sqrt{3}}}{\sqrt{3}} \frac{2\sqrt{2 + \sqrt{3}} - 2\sqrt{6} + \sqrt{6 + 3\sqrt{3}} - \sqrt[]{6 - 3\sqrt{3}}}{\sqrt{3}}](/latexrender/pictures/db385710397671a0bf594f13dd866af4.png)
Você errou essa última passagem. O correto seria:
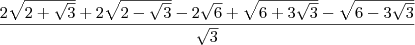
Racionalizando o denominador, temos que:
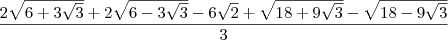
Essa expressão será equivalente a algum número. Vamos chamar esse número de x. Temos então:
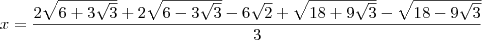
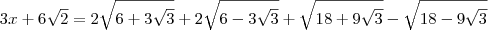
Elevando ambos os membros da equação ao quadrado, temos que:
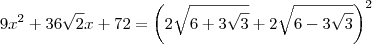
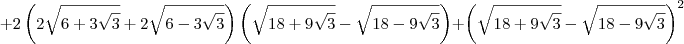
Vamos desenvolver separadamente cada uma das partes que aparecem no segundo membro da equação.
Parte 1)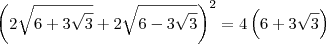
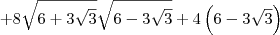
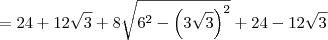
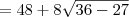
= 72
Parte 2)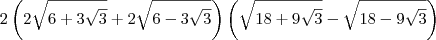
![= 4\left(\sqrt{6 + 3\sqrt{3}}+ \sqrt{6 - 3\sqrt{3}}\right)\left[\sqrt{3}\left(\sqrt{6 + 3\sqrt{3}} - \sqrt{6 - 3\sqrt{3}}\right)\right] = 4\left(\sqrt{6 + 3\sqrt{3}}+ \sqrt{6 - 3\sqrt{3}}\right)\left[\sqrt{3}\left(\sqrt{6 + 3\sqrt{3}} - \sqrt{6 - 3\sqrt{3}}\right)\right]](/latexrender/pictures/f3244a2c11d146dfc031e7970c6b8d07.png)
![= 4\sqrt{3}\left[\left(\sqrt{6 + 3\sqrt{3}}\right)^2 - \left(\sqrt{6 - 3\sqrt{3}}\right)^2\right] = 4\sqrt{3}\left[\left(\sqrt{6 + 3\sqrt{3}}\right)^2 - \left(\sqrt{6 - 3\sqrt{3}}\right)^2\right]](/latexrender/pictures/ccb61b040cd8b2178a62c48f63da13c8.png)
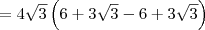
= 72
Parte 3)![\left(\sqrt{18 + 9\sqrt{3}} - \sqrt{18 - 9\sqrt{3}}\right)^2 = \left[\sqrt{3}\left(\sqrt{6 + 3\sqrt{3}} - \sqrt{6 - 3\sqrt{3}}\right)\right]^2 \left(\sqrt{18 + 9\sqrt{3}} - \sqrt{18 - 9\sqrt{3}}\right)^2 = \left[\sqrt{3}\left(\sqrt{6 + 3\sqrt{3}} - \sqrt{6 - 3\sqrt{3}}\right)\right]^2](/latexrender/pictures/bea44d2650b15af1cc17b8b381c434eb.png)
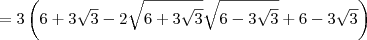
![= 3\left[12 - 2\sqrt{6^2 - \left(3\sqrt{3}\right)^2}\right] = 3\left[12 - 2\sqrt{6^2 - \left(3\sqrt{3}\right)^2}\right]](/latexrender/pictures/22e38c011ff4c9f129967f3e21ea5574.png)
![= 3\left[12 - 2\sqrt{36 - 27}\right] = 3\left[12 - 2\sqrt{36 - 27}\right]](/latexrender/pictures/240d76de4c8e260dd29409bfbf4997f1.png)
= 18
Substituindo os valores das partes na equação, temos que:
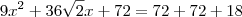
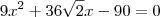
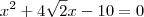
Resolvendo essa equação, obtemos
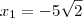
e

.
Analisando a expressão numérica original, percebemos que ela deve ser positiva. Portanto, a única possibilidade válida é
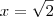
.
nathyn escreveu:2-) Calcule o valor de x sendo,
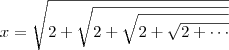
Elevando ambos os membros ao quadrado, temos que:
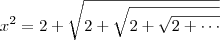
As reticências que aparecem dentro do radical, representam que podemos continuar o desenvolvimento da expressão seguindo o mesmo padrão. Sendo assim, podemos escrever que:
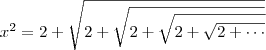
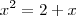

Resolvendo essa equação, temos que

e
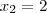
.
Como x é o resultado de uma raiz quadrada, ele deve ser um valor positivo. Portanto, a única possibilidade válida é x = 2.
![\frac{2 + \sqrt[]{3}}{\sqrt[]{2} + \sqrt[]{2 + \sqrt[]{3}}} + \frac{2 - \sqrt[]{3}}{\sqrt[]{2} - \sqrt[]{2 - \sqrt[]{3}}} \frac{2 + \sqrt[]{3}}{\sqrt[]{2} + \sqrt[]{2 + \sqrt[]{3}}} + \frac{2 - \sqrt[]{3}}{\sqrt[]{2} - \sqrt[]{2 - \sqrt[]{3}}}](/latexrender/pictures/9b4c6786a084bd620c64b381db12716f.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
![\frac{\left(2 + \sqrt[]{3} \right)\left(\sqrt[]{2} - \sqrt[]{2 + \sqrt[]{3}} \right)}{2 - 2 -\sqrt[]{3}} + \frac{\left(2 - \sqrt[]{3} \right)\left(\sqrt[]{2} + \sqrt[]{2 - \sqrt[]{3}} \right)}{2 - 2 +\sqrt[]{3}} \frac{\left(2 + \sqrt[]{3} \right)\left(\sqrt[]{2} - \sqrt[]{2 + \sqrt[]{3}} \right)}{2 - 2 -\sqrt[]{3}} + \frac{\left(2 - \sqrt[]{3} \right)\left(\sqrt[]{2} + \sqrt[]{2 - \sqrt[]{3}} \right)}{2 - 2 +\sqrt[]{3}}](/latexrender/pictures/c156b2440bf122cb7cbc7eeafcbe3205.png)
![- \sqrt[]{3} - \sqrt[]{3}](/latexrender/pictures/5146764d594e41cc1e0df3c201b01a02.png) , o sinal do numerador da primeira foram mudados, ficando:
, o sinal do numerador da primeira foram mudados, ficando:![\frac{-2 \sqrt[]{2} + 2\sqrt[]{2 + \sqrt[]{3}} -\sqrt[]{6} + \sqrt[]{6 + 3\sqrt[]{3}}}{\sqrt[]{3}} + \frac{2 \sqrt[]{2} + 2\sqrt[]{2 - \sqrt[]{3}} -\sqrt[]{6} - \sqrt[]{6 - 3\sqrt[]{3}}}{\sqrt[]{3}} \frac{-2 \sqrt[]{2} + 2\sqrt[]{2 + \sqrt[]{3}} -\sqrt[]{6} + \sqrt[]{6 + 3\sqrt[]{3}}}{\sqrt[]{3}} + \frac{2 \sqrt[]{2} + 2\sqrt[]{2 - \sqrt[]{3}} -\sqrt[]{6} - \sqrt[]{6 - 3\sqrt[]{3}}}{\sqrt[]{3}}](/latexrender/pictures/b4435ab6b21a3b089fcf9ce7455b9d0a.png)
![\frac{2\sqrt[]{2 + \sqrt[]{3}} - 2\sqrt[]{6} + \sqrt[]{6 + 3\sqrt[]{3}} - \sqrt[]{6 - 3\sqrt[]{3}}}{\sqrt[]{3}} \frac{2\sqrt[]{2 + \sqrt[]{3}} - 2\sqrt[]{6} + \sqrt[]{6 + 3\sqrt[]{3}} - \sqrt[]{6 - 3\sqrt[]{3}}}{\sqrt[]{3}}](/latexrender/pictures/064eac5f877c0f5c68ae7391c1b032a1.png)
![\frac{2\sqrt[]{6 + 3\sqrt[]{3}} -6\sqrt[]{2} + \sqrt[]{18 + 9\sqrt[]{3}} - \sqrt[]{18 - 9\sqrt[]{3}}}{3} \frac{2\sqrt[]{6 + 3\sqrt[]{3}} -6\sqrt[]{2} + \sqrt[]{18 + 9\sqrt[]{3}} - \sqrt[]{18 - 9\sqrt[]{3}}}{3}](/latexrender/pictures/57d4664c62c4af3e7dd33bd2a9571f49.png)
![x = \sqrt[]{2 + \sqrt[]{2 + \sqrt[]{2 + \sqrt[]{2 + ...}}}} x = \sqrt[]{2 + \sqrt[]{2 + \sqrt[]{2 + \sqrt[]{2 + ...}}}}](/latexrender/pictures/f3d74d2ceb01df84aad6fab06d832cda.png)


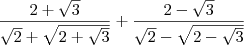
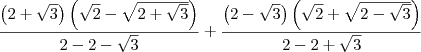
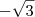 , o sinal do numerador da primeira foram mudados, ficando:
, o sinal do numerador da primeira foram mudados, ficando: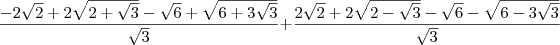
![\frac{2\sqrt{2 + \sqrt{3}} - 2\sqrt{6} + \sqrt{6 + 3\sqrt{3}} - \sqrt[]{6 - 3\sqrt{3}}}{\sqrt{3}} \frac{2\sqrt{2 + \sqrt{3}} - 2\sqrt{6} + \sqrt{6 + 3\sqrt{3}} - \sqrt[]{6 - 3\sqrt{3}}}{\sqrt{3}}](/latexrender/pictures/db385710397671a0bf594f13dd866af4.png)
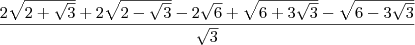
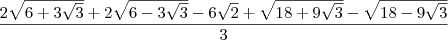
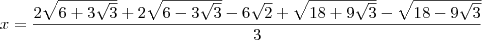
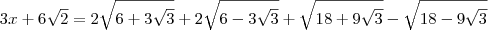
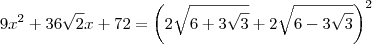
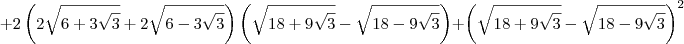
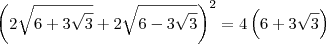
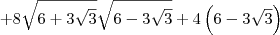
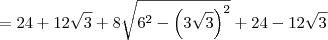
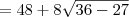
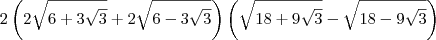
![= 4\left(\sqrt{6 + 3\sqrt{3}}+ \sqrt{6 - 3\sqrt{3}}\right)\left[\sqrt{3}\left(\sqrt{6 + 3\sqrt{3}} - \sqrt{6 - 3\sqrt{3}}\right)\right] = 4\left(\sqrt{6 + 3\sqrt{3}}+ \sqrt{6 - 3\sqrt{3}}\right)\left[\sqrt{3}\left(\sqrt{6 + 3\sqrt{3}} - \sqrt{6 - 3\sqrt{3}}\right)\right]](/latexrender/pictures/f3244a2c11d146dfc031e7970c6b8d07.png)
![= 4\sqrt{3}\left[\left(\sqrt{6 + 3\sqrt{3}}\right)^2 - \left(\sqrt{6 - 3\sqrt{3}}\right)^2\right] = 4\sqrt{3}\left[\left(\sqrt{6 + 3\sqrt{3}}\right)^2 - \left(\sqrt{6 - 3\sqrt{3}}\right)^2\right]](/latexrender/pictures/ccb61b040cd8b2178a62c48f63da13c8.png)
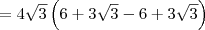
![\left(\sqrt{18 + 9\sqrt{3}} - \sqrt{18 - 9\sqrt{3}}\right)^2 = \left[\sqrt{3}\left(\sqrt{6 + 3\sqrt{3}} - \sqrt{6 - 3\sqrt{3}}\right)\right]^2 \left(\sqrt{18 + 9\sqrt{3}} - \sqrt{18 - 9\sqrt{3}}\right)^2 = \left[\sqrt{3}\left(\sqrt{6 + 3\sqrt{3}} - \sqrt{6 - 3\sqrt{3}}\right)\right]^2](/latexrender/pictures/bea44d2650b15af1cc17b8b381c434eb.png)
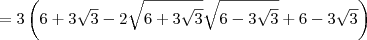
![= 3\left[12 - 2\sqrt{6^2 - \left(3\sqrt{3}\right)^2}\right] = 3\left[12 - 2\sqrt{6^2 - \left(3\sqrt{3}\right)^2}\right]](/latexrender/pictures/22e38c011ff4c9f129967f3e21ea5574.png)
![= 3\left[12 - 2\sqrt{36 - 27}\right] = 3\left[12 - 2\sqrt{36 - 27}\right]](/latexrender/pictures/240d76de4c8e260dd29409bfbf4997f1.png)
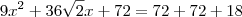
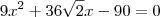
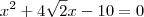
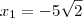 e
e  .
.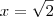 .
.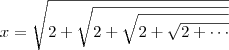
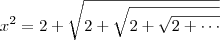
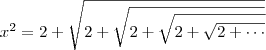
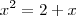

 e
e 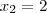 .
.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)