![\sqrt[3]{\frac{a}{b}\sqrt[]{\frac{a}{b}}} \sqrt[3]{\frac{a}{b}\sqrt[]{\frac{a}{b}}}](/latexrender/pictures/23a4ae54d10ad257dbb343d12ef15367.png)
Resposta :
![\sqrt[]{\frac{a}{b}} \sqrt[]{\frac{a}{b}}](/latexrender/pictures/42e6680459316c84bb1fb8314be42226.png)
O que eu tentei fazer :
![\sqrt[3]{\frac{a}{b}.{\frac{a}{b}}^{\frac{1}{2}}} \sqrt[3]{\frac{a}{b}.{\frac{a}{b}}^{\frac{1}{2}}}](/latexrender/pictures/4c0a68a36d6923ca02ffcc9e2a7dbc9d.png) =
= 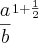 =
= 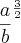
=
![\sqrt[3]{\sqrt[]{{\frac{a}{b}}^{3}}} \sqrt[3]{\sqrt[]{{\frac{a}{b}}^{3}}}](/latexrender/pictures/259287c25e3eb8fcda18c5eb3c45dc33.png) =
= ![\sqrt[6]{{\frac{a}{b}}^{3}}} \sqrt[6]{{\frac{a}{b}}^{3}}}](/latexrender/pictures/9cc1c7f76a4271e17adb409c83c3d44d.png)
2- O número
![3+2\sqrt[]{2} 3+2\sqrt[]{2}](/latexrender/pictures/8a4f488b4902771b4ebfb90b4b32531b.png) é igual a raíz quadrada de:
é igual a raíz quadrada de:Aí entre as opções dadas a resposta certa é
![17+12\sqrt[]{2} 17+12\sqrt[]{2}](/latexrender/pictures/814ff90ef7adadf59742a2e08edbae67.png)
Nessa eu tentei desenvolver a partir da resposta pra chegar na conta que tá no enunciado
![\sqrt[]{17+12\sqrt[]{2}} \sqrt[]{17+12\sqrt[]{2}}](/latexrender/pictures/4a23c1c92127489738607eae78cecb15.png)
Nessa conta eu tentei jogar o 12 pra dentro da raiz e depois tentei tranformar a raiz em potência, mas não consegui desenvolver.
3-

Bom, comecei fazendo assim :
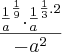
=

Tá certo? dá pra continuar daí?
Vlw pessoal





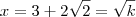 . Agora, basta elevar a o quadrado para encontrar o número k.
. Agora, basta elevar a o quadrado para encontrar o número k.
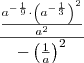
 .
.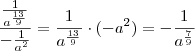 .
.

![\sqrt[3]{\frac{a}{b}\sqrt{\frac{a}{b}}} \Rightarrow \sqrt[3]{\frac{a}{b}.\frac{a^{\frac12}}{b^{\frac12}}} \sqrt[3]{\frac{a}{b}\sqrt{\frac{a}{b}}} \Rightarrow \sqrt[3]{\frac{a}{b}.\frac{a^{\frac12}}{b^{\frac12}}}](/latexrender/pictures/ea24b276823e85d84043e06a76af0e7a.png)

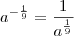 . O mesmo vale para o que está entre parênteses.
. O mesmo vale para o que está entre parênteses.
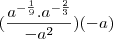
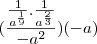
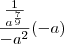

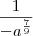
![\frac{a}{\sqrt[9]{-a^7}} \frac{a}{\sqrt[9]{-a^7}}](/latexrender/pictures/1f3b74b1d4f35bd0ac31e68e1f5a8b23.png)

![\sqrt[3]{{\frac{a}{b}}^{\frac{3}{2}}} \sqrt[3]{{\frac{a}{b}}^{\frac{3}{2}}}](/latexrender/pictures/df1b16fd03be1b446154cac49e152b65.png)
![\sqrt[3]{\sqrt[]{{\left( \frac{a}{b} \right)}^{3}}} \sqrt[3]{\sqrt[]{{\left( \frac{a}{b} \right)}^{3}}}](/latexrender/pictures/f02a854bd15f1d2eea4ae842d540c99c.png)
![\sqrt[6]{{\left( \frac{a}{b} \right)}^{3}} \sqrt[6]{{\left( \frac{a}{b} \right)}^{3}}](/latexrender/pictures/3f2aa6945c3a715f3329ce88e7bf4afb.png)

![\sqrt[3]{({\frac{a}{b}})^{\frac{3}{2}}} \sqrt[3]{({\frac{a}{b}})^{\frac{3}{2}}}](/latexrender/pictures/ffd57e44d1b14cc3dc3e0219fa489f20.png)
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)