provar que:
Fn²=(Fn-1).F(n+1)+ (-1)^n+1
comecei assim:
1-1-2-3-5-8-13-21-34-55-89
para n=3.
F(3)=2.
F(2)=1
F(4)=3
2²=1.3+1->4=4,ok!
para n=k.
Fk²=F(k-1).F(k+1)+(-1)^k+1
para n=k+1.
F(k+1)²=F(k+1-1).F(k+1+1)+(-1)^k+1+1
F(k²+2k+1)=Fk.F(k+2)+(-1)^k
Oque eu faço agora?Tenho que provar a igualdade.
não usei o editor de fórmulas porque tenho que sair agora.^^
Se alguém me ajudar fico grata!


 temos,
temos,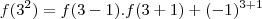
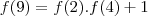
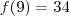

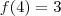
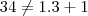

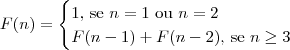 , com
, com ![[F(n)]^2 = F(n-1)\cdot F(n+1) + (-1)^{n+1} [F(n)]^2 = F(n-1)\cdot F(n+1) + (-1)^{n+1}](/latexrender/pictures/77165280e52812c898598817e2ca0cb2.png) , com
, com ![[F(n+1)]^2 =F(n)\cdot F(n+2) + (-1)^{n+2} [F(n+1)]^2 =F(n)\cdot F(n+2) + (-1)^{n+2}](/latexrender/pictures/cc7021783968a7c61a47e2100f0b4a57.png) .
.![F(n)\cdot F(n+2) + (-1)^{n+2} = F(n)\cdot [F(n+1)+F(n)] + (-1)^{n+1}(-1) F(n)\cdot F(n+2) + (-1)^{n+2} = F(n)\cdot [F(n+1)+F(n)] + (-1)^{n+1}(-1)](/latexrender/pictures/3e13416c50496e4d0438a6de2b2b87de.png)
![= F(n)\cdot F(n+1)+ [F(n)]^2 - (-1)^{n+1} = F(n)\cdot F(n+1)+ [F(n)]^2 - (-1)^{n+1}](/latexrender/pictures/d7504164fe96432169c1510e25086b98.png) (nesse passo usamos a hipótese de indução)
(nesse passo usamos a hipótese de indução)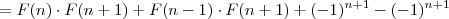
![= [F(n)+ F(n-1)]\cdot F(n+1) = [F(n)+ F(n-1)]\cdot F(n+1)](/latexrender/pictures/96cd04e3f7dd212a61989d738c42361e.png)
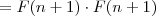
![= [F(n+1)]^2 = [F(n+1)]^2](/latexrender/pictures/09822388b63275cdfa3c223f191cb047.png)


 .
.



