 por Abelardo » Sáb Abr 09, 2011 18:48
por Abelardo » Sáb Abr 09, 2011 18:48
57. Considerando a e b quaisquer números reais que sastifazem à condição
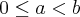
julgue os itens que se seguem:
1)
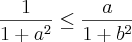
2)
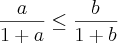
3)
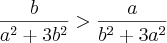
4)
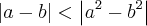
A primeira, segunda e a terceira eu fiz tranquilo, mas a terceira não consegui. Se quiserem, podem apresentar a solução de todas, é bom saber outras formas também para resolver as questões!
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
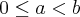 julgue os itens que se seguem:
julgue os itens que se seguem: 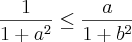
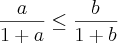
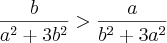
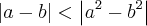

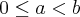 julgue os itens que se seguem:
julgue os itens que se seguem: 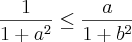
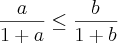
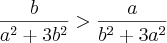
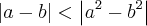


 .
.



