83) Mostre que existem
 e
e  racionais tais que
racionais tais que ![\sqrt[]{18 - 8 \sqrt[]{2}}=a + b\sqrt[]{2} \sqrt[]{18 - 8 \sqrt[]{2}}=a + b\sqrt[]{2}](/latexrender/pictures/8ea859c3d9626f90602be68cf7a92993.png)
84)Dados dois números x e y reais e positivos, chama-se média aritmética de x com y o real
 e chama-se média geométrica o real
e chama-se média geométrica o real ![g=\sqrt[]{xy} g=\sqrt[]{xy}](/latexrender/pictures/1b1a50a0e8fd3637db98a6830e1470f7.png) . Mostre que
. Mostre que  para todos
para todos 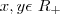
87) Prove que, dado um número racional
 e um número natural
e um número natural  , nem sempre
, nem sempre ![\sqrt[n]{\frac{a}{b}} \sqrt[n]{\frac{a}{b}}](/latexrender/pictures/317d53501ad6cd19416e2938df2defda.png) é racional.
é racional.Qualquer dica é bem vinda!


![(\sqrt[2]{x} - \sqrt[2]{y})^{2} (\sqrt[2]{x} - \sqrt[2]{y})^{2}](/latexrender/pictures/a3ce79d5e19e738e0eacb09a845a3ff0.png) , perceba que como está ao quadrado,e , pelo enunciado, X e Y são numeros positivos, é claro que isso resultará em um numero positivo, ou igual a zero, logo:
, perceba que como está ao quadrado,e , pelo enunciado, X e Y são numeros positivos, é claro que isso resultará em um numero positivo, ou igual a zero, logo:![(\sqrt[2]{x} - \sqrt[2]{y})^{2} \geq 0 (\sqrt[2]{x} - \sqrt[2]{y})^{2} \geq 0](/latexrender/pictures/e4bb14558001f03a4ecc4875acf7ef06.png)
![x - 2\sqrt[2]{x.y} + y \geq 0 x - 2\sqrt[2]{x.y} + y \geq 0](/latexrender/pictures/343e2cb2e73652d1c1d7e6c2a9e3fee8.png)
![x + y \geq 2\sqrt[2]{x.y} x + y \geq 2\sqrt[2]{x.y}](/latexrender/pictures/bd88f98b2d6ee2b9dd8ad200a1721cca.png)
![\frac{x + y}{2} \geq \sqrt[2]{x.y} \frac{x + y}{2} \geq \sqrt[2]{x.y}](/latexrender/pictures/f8301043239b4da55c1020c502f89f4b.png)

![(\sqrt[]{x} - \sqrt[]{y})^{2} \geq 0 (\sqrt[]{x} - \sqrt[]{y})^{2} \geq 0](/latexrender/pictures/ffe2bb4c12e165178931fe1847358ca4.png)
![x - 2\sqrt[]{xy} + y \geq 0 x - 2\sqrt[]{xy} + y \geq 0](/latexrender/pictures/63a2bc12f64238ed09f09c1cb923d6f1.png)
![x + y \geq 2\sqrt[]{xy} x + y \geq 2\sqrt[]{xy}](/latexrender/pictures/23d8f461a3c98fbc5a3f80a11c577629.png)
![\frac{x + y}{2} \geq \sqrt[]{xy} \frac{x + y}{2} \geq \sqrt[]{xy}](/latexrender/pictures/c4e99408f0f0406541504852b31eabae.png)
 e
e  pois
pois ![18 - 8 \sqrt[]{2} = \left(4 - \sqrt{2}\right)^2 18 - 8 \sqrt[]{2} = \left(4 - \sqrt{2}\right)^2](/latexrender/pictures/f5b7911bad8580b70f99f0fb6e895725.png) .
.
![a +\sqrt[]{2}.(b+1)=4 a +\sqrt[]{2}.(b+1)=4](/latexrender/pictures/791a399f862228e71443b314d816614f.png) . Mas tenho um livro que diz: ''Para construção de irracionais é usar o fato de que, se
. Mas tenho um livro que diz: ''Para construção de irracionais é usar o fato de que, se  é irracional e
é irracional e  é racional não nulo, então:
é racional não nulo, então: 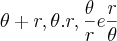 são todos irracionais..
são todos irracionais..  . Logo
. Logo 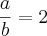 . Então
. Então ![\sqrt[2]{\frac{a}{b}}=\sqrt[2]{2} \sqrt[2]{\frac{a}{b}}=\sqrt[2]{2}](/latexrender/pictures/bdc4db9376e309fac3e6bdd7fb5638fa.png) , onde raiz quadrada de dois é um irracional(Desculpe-me Professor Aquino, a questão estava incompleta mesmo)
, onde raiz quadrada de dois é um irracional(Desculpe-me Professor Aquino, a questão estava incompleta mesmo)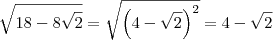 . Lembrando que essa última simplificação só pode ser feita dese jeito pois
. Lembrando que essa última simplificação só pode ser feita dese jeito pois 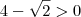 . Sendo assim, no exercício temos que
. Sendo assim, no exercício temos que  , nem sempre
, nem sempre 
 .
.



