 por Young » Sáb Set 06, 2008 15:42
por Young » Sáb Set 06, 2008 15:42
Olá! Estou no primeiro período do curso de Estatística e estou tendo uma grande dificuldade com a disciplina de Álgebra, principalmente na parte de Conjuntos.
Estou tentando fazer o seguinte exercício:
Sejam

conjuntos, então demonstre que
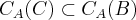 (Complementar de C em A está contido em Complementar de B em A)
(Complementar de C em A está contido em Complementar de B em A)Tentei resolver da seguinte forma:
Seja

, temos
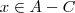
, logo
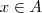
e

não

.
Como

, então também podemos dizer que
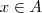
e

não
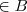
Daí
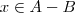
Então como

, temos
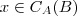
Com isso,
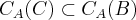
Não sei se está certa essa linha de raciocínio... Se alguem puder me dar uma ajuda!
Desde já obrigado!

Ps: Não consegui demonstrar o símbolo "Não Pertence" através do LaTeX.
-
Young
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Set 06, 2008 15:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Estatística
- Andamento: cursando
 por admin » Ter Set 09, 2008 16:11
por admin » Ter Set 09, 2008 16:11
Olá
Young, boas-vindas!
Pela minha formação não sou habilitado a sanar dúvidas da graduação, então sempre assumo um posicionamento de aluno.
Espero que logo tenhamos algum colaborador professor universitário.
Mas, acredito que seu raciocínio esteja sim correto.
Sobre o símbolo:

- Código: Selecionar todos
\notin
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Diferença simétrica
por Incognite » Sáb Mar 10, 2018 18:22
- 1 Respostas
- 3558 Exibições
- Última mensagem por adauto martins

Qui Abr 26, 2018 20:15
Conjuntos
-
- Dúvidas - Conjuntos
por joaopedrel » Sáb Mar 13, 2010 23:06
- 2 Respostas
- 2131 Exibições
- Última mensagem por joaopedrel

Dom Mar 14, 2010 19:54
Conjuntos
-
- Dúvidas Conjuntos
por Andrewo » Qui Abr 12, 2012 09:12
- 8 Respostas
- 4663 Exibições
- Última mensagem por Andrewo

Sex Abr 13, 2012 14:46
Conjuntos
-
- [Conjuntos] Dúvidas no exercício.
por HeidyTrinidad » Sex Abr 11, 2014 10:35
- 1 Respostas
- 1801 Exibições
- Última mensagem por e8group

Sex Abr 11, 2014 18:16
Conjuntos
-
- Dúvidas Teoria dos Conjuntos
por GabrielSilv0 » Seg Set 21, 2015 14:59
- 1 Respostas
- 1608 Exibições
- Última mensagem por nakagumahissao

Dom Out 04, 2015 12:59
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 conjuntos, então demonstre que
conjuntos, então demonstre que 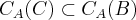 (Complementar de C em A está contido em Complementar de B em A)
(Complementar de C em A está contido em Complementar de B em A), temos
, logo
e
não
.
, então também podemos dizer que
e
não
, temos


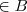
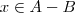
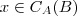



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.