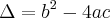por stanley tiago » Sáb Jan 22, 2011 12:16
por stanley tiago » Sáb Jan 22, 2011 12:16
determine os coeficientes de x² de de x , nas seguintes equaçoes literais
a)
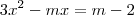
R: 3 ; - m
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por stanley tiago » Sáb Jan 22, 2011 12:40
por stanley tiago » Sáb Jan 22, 2011 12:40
bom , vou colocar aqui minha tentativas
![3x^2-mx=m-2
3x^2=m-2+mx
3x^2=m(-2+x)
x= \sqrt[]{m(-2+x)\frac{}{3}} 3x^2-mx=m-2
3x^2=m-2+mx
3x^2=m(-2+x)
x= \sqrt[]{m(-2+x)\frac{}{3}}](/latexrender/pictures/4df02e7401ab57ce4a20b599000cd727.png)
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por VtinxD » Sáb Jan 22, 2011 14:23
por VtinxD » Sáb Jan 22, 2011 14:23
O Coeficiente de um termo da equação é a constante a qual ele está multiplicado.Considere a sua equação:

.Perceba que o termo

está multiplicado por 3 e que

está multiplicado por -m.
Espero ter ajudado
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por stanley tiago » Sáb Jan 22, 2011 15:36
por stanley tiago » Sáb Jan 22, 2011 15:36
é por esse caminho ? eu ja tentei tirar o x em evidencia mais nao tive muito sucesso .
e em tirar o m em evidecia tbm nao tive êxito.

x(3x-m)-(m-2)=0
x(3x-m-m+2)=0
x (3x-2m+2)=0
x= 0/(3x-2m+2)
x=0
ou a soluçao pra equçao é usando o discriminante
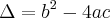
com a = 3 ; b = -m ; c = -(m-2)
por favor me diga qual desse caminhos a seguir
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Sáb Jan 22, 2011 16:03
por Molina » Sáb Jan 22, 2011 16:03
Boa tarde,
Os coeficientes de x² e x você já tem. São eles: 3 e -m.
É só isso que o problema quer, que você os identifique.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por stanley tiago » Sáb Jan 22, 2011 16:19
por stanley tiago » Sáb Jan 22, 2011 16:19
hehe será q eu to tao louco assim q nao percebi q era isso q ele tava me pedindo !!

É. parece q é isso mesmo
obrigado.
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- equações literais do 2°grau
por stanley tiago » Dom Jan 23, 2011 12:19
- 5 Respostas
- 2290 Exibições
- Última mensagem por stanley tiago

Dom Jan 23, 2011 17:24
Álgebra Elementar
-
- equações de 2º grau
por Lismara » Seg Ago 31, 2009 23:25
- 4 Respostas
- 2854 Exibições
- Última mensagem por Lismara

Ter Set 01, 2009 21:42
Sistemas de Equações
-
- Equações 2º Grau
por Quatroemes » Dom Mar 21, 2010 20:53
- 2 Respostas
- 2630 Exibições
- Última mensagem por Quatroemes

Seg Mar 22, 2010 11:34
Funções
-
- equacoes do 2 Grau
por guillcn » Qui Jun 30, 2011 12:30
- 1 Respostas
- 1603 Exibições
- Última mensagem por joaofonseca

Qui Jun 30, 2011 15:25
Equações
-
- equaçoes do 1 grau
por thalia alexandrina » Seg Out 10, 2011 14:29
- 3 Respostas
- 3027 Exibições
- Última mensagem por MarceloFantini

Ter Out 11, 2011 23:06
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
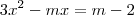

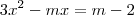

![3x^2-mx=m-2
3x^2=m-2+mx
3x^2=m(-2+x)
x= \sqrt[]{m(-2+x)\frac{}{3}} 3x^2-mx=m-2
3x^2=m-2+mx
3x^2=m(-2+x)
x= \sqrt[]{m(-2+x)\frac{}{3}}](/latexrender/pictures/4df02e7401ab57ce4a20b599000cd727.png)

 .Perceba que o termo
.Perceba que o termo  está multiplicado por 3 e que
está multiplicado por 3 e que  está multiplicado por -m.
está multiplicado por -m.