Sei que aqui é a área de Álgebra elementar, mas não sei exatamente onde postar as minhas dúvidas em Álgebra abstrata, então resolvi criar o tópico aqui mesmo, qualquer problema por favor mudem o tópico de lugar.
Alguém poderia verificar se a demonstração que fiz está correta ?
Sejam
 o Maior Divisor Comum deles.
o Maior Divisor Comum deles.Já que
 é um ideal de
é um ideal de  , então, pelo visto acima, existe
, então, pelo visto acima, existe  tal que
tal que  .
. Mostre que
 e portanto que existem
e portanto que existem 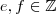 tais que
tais que  .
.Desenvolvimento:
Sendo
 , temos:
, temos: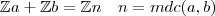
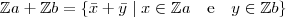
Agora tomemos um elemento
 tal que
tal que 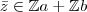 , então:
, então: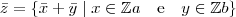
Então temos:
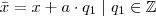
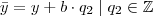
Logo:

![\bar{x} + \bar{y} = x + y + mdc(a,b) \cdot [c_{1} \cdot q_{1} + c_{2} \cdot q_{2}] \bar{x} + \bar{y} = x + y + mdc(a,b) \cdot [c_{1} \cdot q_{1} + c_{2} \cdot q_{2}]](/latexrender/pictures/05fd58e774f06081f66fe3c1223043f5.png)
Onde
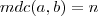 e
e  e chamaremos de
e chamaremos de  o termo
o termo ![[c_{1} \cdot q_{1} + c_{2} \cdot q_{2}] [c_{1} \cdot q_{1} + c_{2} \cdot q_{2}]](/latexrender/pictures/81d5c6638da602680b5fa7fd694dfa2a.png) .
.Então teremos:
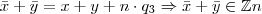

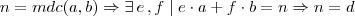


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)