 por Carolziiinhaaah » Sáb Jun 19, 2010 01:11
por Carolziiinhaaah » Sáb Jun 19, 2010 01:11
Determinar p e q de modo que a equação

, apresente duas raízes recíprocas entre si e as outras duas com soma igual a 1.
gabarito:
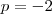
e

-

Carolziiinhaaah
- Usuário Parceiro

-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Douglasm » Dom Jun 20, 2010 09:23
por Douglasm » Dom Jun 20, 2010 09:23
Esse problema, ao meu ver é mais teórico. Note que a definição de equação recíproca é:
*Dizemos que uma equação polinomial é recíproca se, quando o número k atende à equação, tivermos que 1/k também atende. (Matemática em Nível IME/ITA - Caio Guimarães)
Por conta disso, é fácil notar que esta é uma recíproca de 2ª espécie (coeficientes equidistantes do "centro" possuem módulos iguais e sinais opostos) e que, consequentemente:
p = -2
q = 0
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Carolziiinhaaah » Seg Jun 21, 2010 19:19
por Carolziiinhaaah » Seg Jun 21, 2010 19:19
Entendi sua explicação, Douglas.. mas não a resolução da questão. Entao, nesse caso, o

não deveria assumir o valor de

, e o

tbm? :/
-

Carolziiinhaaah
- Usuário Parceiro

-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [polinômio]Relações de Girard + raízes de polinômio
por matano2104 » Qui Set 05, 2013 17:02
- 1 Respostas
- 7155 Exibições
- Última mensagem por young_jedi

Qui Set 05, 2013 17:57
Polinômios
-
- Equação Algébrica
por Carolziiinhaaah » Qui Jun 03, 2010 17:30
- 2 Respostas
- 2270 Exibições
- Última mensagem por Carolziiinhaaah

Seg Jun 14, 2010 14:05
Álgebra Elementar
-
- Equação Algébrica de raiz dupla
por Carolziiinhaaah » Sáb Jun 19, 2010 01:16
- 1 Respostas
- 1752 Exibições
- Última mensagem por Douglasm

Dom Jun 20, 2010 09:39
Álgebra Elementar
-
- [equaçao algebrica] travei na resoluçao
por vera lucia » Ter Set 20, 2011 00:08
- 2 Respostas
- 1616 Exibições
- Última mensagem por MarceloFantini

Ter Set 20, 2011 18:38
Funções
-
- [equaçao algebrica] travei na resoluçao
por vera lucia » Ter Set 20, 2011 00:08
- 1 Respostas
- 1293 Exibições
- Última mensagem por Neperiano

Ter Set 20, 2011 13:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , apresente duas raízes recíprocas entre si e as outras duas com soma igual a 1.
, apresente duas raízes recíprocas entre si e as outras duas com soma igual a 1. e
e 

 , apresente duas raízes recíprocas entre si e as outras duas com soma igual a 1.
, apresente duas raízes recíprocas entre si e as outras duas com soma igual a 1. e
e 


 não deveria assumir o valor de
não deveria assumir o valor de  , e o
, e o  tbm? :/
tbm? :/


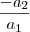 )
)

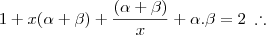

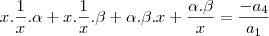

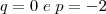
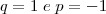

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
