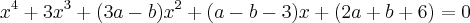 admita duas e somente duas raízes nulas.
admita duas e somente duas raízes nulas.

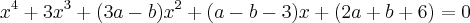 admita duas e somente duas raízes nulas.
admita duas e somente duas raízes nulas.
 tem duas de suas raízes iguais a zero. Isso significa que quando substituímos
tem duas de suas raízes iguais a zero. Isso significa que quando substituímos  na equação proposta, esta deverá resultar em zero. Também sabemos que somente duas de suas raízes são zero. Se essa informação não nos fosse dada, poderíamos admitir que essa equação teria todas as suas raízes iguais a zero (lembre-se que se um número complexo é raiz de uma equação então o seu conjugado também é raiz dessa equação).
na equação proposta, esta deverá resultar em zero. Também sabemos que somente duas de suas raízes são zero. Se essa informação não nos fosse dada, poderíamos admitir que essa equação teria todas as suas raízes iguais a zero (lembre-se que se um número complexo é raiz de uma equação então o seu conjugado também é raiz dessa equação).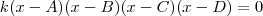 , onde A, B, C e D são raízes da equação e
, onde A, B, C e D são raízes da equação e 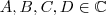 .
. 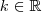 e é o termo que acompanha o termo de maior grau da equação. Da equação proposta no enunciado temos que
e é o termo que acompanha o termo de maior grau da equação. Da equação proposta no enunciado temos que  . Como nós temos duas raízes nulas façamos
. Como nós temos duas raízes nulas façamos 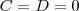 . Teremos então a expressão
. Teremos então a expressão 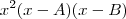 que é semelhante à expressão
que é semelhante à expressão 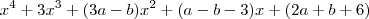 . Então:
. Então:
![x^2[x^2-(A+B)x+AB]\equiv x^4+3x^3+(3a-b)x^2+(a-b-3)x+(2a+b+6) x^2[x^2-(A+B)x+AB]\equiv x^4+3x^3+(3a-b)x^2+(a-b-3)x+(2a+b+6)](/latexrender/pictures/f92a85e02fc67ff9b85ed55df2b5e58d.png)

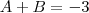
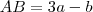





 tenha duas, e somente duas raízes nulas, a e b devem valer, respectivamente,
tenha duas, e somente duas raízes nulas, a e b devem valer, respectivamente,  e
e  .
. 


Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 .
.
 :
: