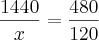Quantas famílias?

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Quantas famílias?

Regras do fórum
Responder

Quantas famílias?

Mensagempor Cleyson007 » Sáb Jan 09, 2010 13:04

Olá, boa tarde!

Resolvi a questão abaixo, mas não encontrei o resultado do gabarito. Alguém pode me ajudar?

Se 12 recenseadores visitam 1440 famílias em 5 dias de trabalho de 8 horas por dia, quantas famílias serão visitadas por 5 recenseadores, em 6 dias, trabalhando 4 horas por dia?

Montei a seguinte tabela:

Imagem

Resolvendo:

\frac{1440}{x}=\left(\frac{12}{5} \right)\left(\frac{6}{5} \right)\left(\frac{8}{4} \right)

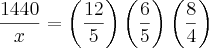
Encontrei x=250.

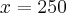
O gabarito aponta 360 famílias como resposta correta.

Até mais.
A Matemática está difícil? Não complica! Mande para cá: descomplicamat@hotmail.com

Imagem
Avatar do usuário
Cleyson007
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 1228
Registrado em: Qua Abr 30, 2008 00:08
Formação Escolar: GRADUAÇÃO
Área/Curso: Matemática UFJF
Andamento: formado
Voltar ao topo

Re: Quantas famílias?

Mensagempor Molina » Sáb Jan 09, 2010 14:14

Boa tarde, Cleyson.

Realmente essas regras de 3 compostas confundem a mente.

Sua tabela é uma boa forma de começar o problema, mas vou fazer de uma forma diferente:

Pelo enunciado, 12 recenseadores visitam 1440 famílias em 5 dias de trabalho de 8 horas por dia. Ou seja, 12 recenseadores, trabalhando 40h (5d*8h), atendem 1440 família.

Continunado o enunciado, temos que 5 recenseadores, em 6 dias, trabalhando 4 horas por dia, atendem x famílias. Ou seja, 5 recenseadores, trabalhando 24h (6d*4h), atendem x famílias.

Agora esses dados que estão sublinhados você vai colocar numa tabela. Note que diminuimos um dado, ficando apenas com o total de horas trabalhadas.

TABELA.JPG

\frac{480}{120}=\frac{1440}{x}\Rightarrow x=360

:y:
Diego Molina | CV | FB | .COM
Equipe AjudaMatemática.com


"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
Avatar do usuário
Molina
Colaborador Moderador - Professor
Colaborador Moderador - Professor
 
Mensagens: 1551
Registrado em: Dom Jun 01, 2008 14:10
Formação Escolar: GRADUAÇÃO
Área/Curso: Licenciatura em Matemática - UFSC
Andamento: formado
Voltar ao topo

Re: Quantas famílias?

Mensagempor Cleyson007 » Sáb Jan 09, 2010 17:18

Boa tarde Molina!

Realmente, por esse método é bem mais fácil e menos confuso!

Não havia pensado dessa forma..

Analisando sua resolução, constatei que reduziu a regra à três colunas. Pelo que pude perceber, ainda dava para reduzir mais ainda, não é?

Veja: 12 recenseadores estão trabalhando durante 40 horas. Logo, para 1 recenseador fazer todo o serviço precisaria trabalhar (40*12) 480 hs.

Da mesma forma, 5 recenseadores estão trabalhando durante 24 horas. Logo, para 1 recenseador fazer todo o serviço precisaria trabalhar (24*5) 120 hs.

Montando a regra de três, encontra-se o mesmo resultado:

\frac{1440}{x}=\frac{480}{120}

x=360

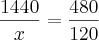
Até mais.
A Matemática está difícil? Não complica! Mande para cá: descomplicamat@hotmail.com

Imagem
Avatar do usuário
Cleyson007
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 1228
Registrado em: Qua Abr 30, 2008 00:08
Formação Escolar: GRADUAÇÃO
Área/Curso: Matemática UFJF
Andamento: formado
Voltar ao topo

Re: Quantas famílias?

Mensagempor Molina » Sáb Jan 09, 2010 18:41

É isso mesmo, dava pra reduzir mais uma vez! :y:
Diego Molina | CV | FB | .COM
Equipe AjudaMatemática.com


"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
Avatar do usuário
Molina
Colaborador Moderador - Professor
Colaborador Moderador - Professor
 
Mensagens: 1551
Registrado em: Dom Jun 01, 2008 14:10
Formação Escolar: GRADUAÇÃO
Área/Curso: Licenciatura em Matemática - UFSC
Andamento: formado
Voltar ao topo
Responder

Voltar para Álgebra Elementar

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: Taxa de variação
Autor: felipe_ad - Ter Jun 29, 2010 19:44

Como resolvo uma questao desse tipo:

Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?

A letra (a) consegui resolver e cheguei no resultado correto de \frac{4\pi{r}^{2}}{3}
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é 1,066\pi

Alguem me ajuda? Agradeço desde já.

Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47

V = (1/3)*pi*r²*h ----> h = 4r/3

V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³

Derivando:

dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3

Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s

Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17

Temos que o volume é dado por:

V = \frac{4\pi}{3}r^2


Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

\frac{dV}{dt} = \frac{8\pi.r}{3}.\frac{dr}{dt}


Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:

\frac{dV}{dt} = \frac{8\pi.2}{3}.\frac{2}{10}

\frac{dV}{dt} = \frac{16\pi}{15}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

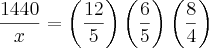
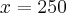Índice do fórum