A questão dá tanta informação que é fácil ficar confuso em qual método de solução investir.
Eu faria assim:
Já que definimos um sistema de eixos x e y, podemos
mapear essa circunferência definindo a equação que a gera. Você deve saber que a equação de uma circunferência de cento no ponto genérico
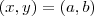
e raio

é
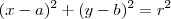
Daí, a nossa circunferência de centro
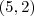
se escreve como
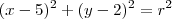
.
Mas, e o raio? Outro ponto foi dado: o ponto A de coordenadas
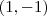
. Portanto, deve ser verdade que
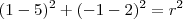
de onde

.
Note que a reta que liga o ponto B ao A é uma contante. Os pontos estão na mesma "altura", com relação ao eixo y. Isto é, as coordenadas de B devem ser
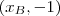
. Com isso, já que B pertence a circunferência, entao
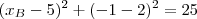
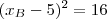
de onde
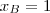
ou
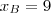
. Mas se
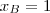
então
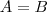
que não reflete a nossa situação. Portanto,
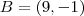
.
Agora, se M é o ponto médio de

, não é difícil de mostrar que
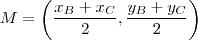
.
Assim,
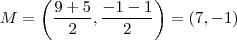
.
Veja que os pontos D e E são pontos que pertencem a circunferência e, ao mesmo tempo, tem ambos coordenada x igual a coordenada x de M!
Portanto, a única forma de
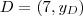
e
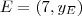
se ajustarem a geometria a qual lhes é sugerida é o cumprimento de
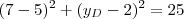
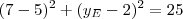
Certo?
Resolvendo, genericamente, a equação
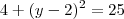
você obtem
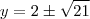
. Como
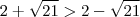
e o ponto D está "mais alto" que E, então
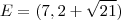
e
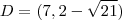
.
Finalmente, a distância esntre eles será, já que compartilham a mesma coordenada x,
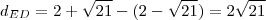


 e raio
e raio  é
é
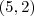 se escreve como
se escreve como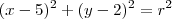 .
.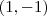 . Portanto, deve ser verdade que
. Portanto, deve ser verdade que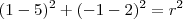
 .
.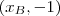 . Com isso, já que B pertence a circunferência, entao
. Com isso, já que B pertence a circunferência, entao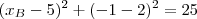
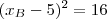
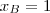 ou
ou 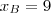 . Mas se
. Mas se 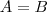 que não reflete a nossa situação. Portanto,
que não reflete a nossa situação. Portanto, 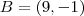 .
. , não é difícil de mostrar que
, não é difícil de mostrar que 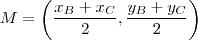 .
. 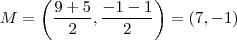 .
.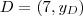 e
e 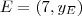 se ajustarem a geometria a qual lhes é sugerida é o cumprimento de
se ajustarem a geometria a qual lhes é sugerida é o cumprimento de 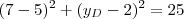
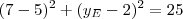
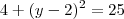
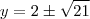 . Como
. Como 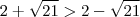 e o ponto D está "mais alto" que E, então
e o ponto D está "mais alto" que E, então 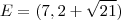 e
e 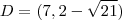 .
.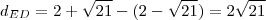


 .
.
 :
: