 por silviopuc » Dom Dez 29, 2013 00:55
por silviopuc » Dom Dez 29, 2013 00:55
Preciso de ajuda para o exercício a seguir. Não soube trabalhar com um trinômio...
A soma dos coeficientes do desenvolvimento de
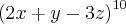
é necessariamente:
a) um número maior que

b) um número entre

e

c) igual a 1
d) igual a zero
e) um número negativo.
-
silviopuc
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Jan 15, 2013 12:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Dom Dez 29, 2013 16:36
por e8group » Dom Dez 29, 2013 16:36
Começamos com a soma de dois números reais

.Esta soma a uma potência

se escreve como
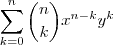
(Teorema Binomial ) e igualdade

nos dá a soma dos coeficientes acima
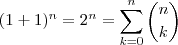
. E quando temos

números reais

,o
teorema multinomial nos garanti uma forma de expandir
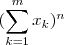
como se vê lá ...
Mas como o objetivo é obter a soma dos coeficientes de

na sua forma expandida . Fazendo todos

iguais a

, teremos

que és a soma requerida .
Justificativa :
Segue-se que

se escreve sob a soma das parcelas que se exprimem por

;

,esta afirmação é assegurada pelo teorema multinomial , ou então notando a fórmula de recorrência :

.Em que a notação

designa a soma dos primeiros

termos da lista
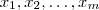
,i.e.,

.
E assim concluindo ,quando fizermos todos os

iguais

teremos a soma dos coeficientes

.
Agora tente concluir.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por silviopuc » Seg Dez 30, 2013 15:28
por silviopuc » Seg Dez 30, 2013 15:28
Santhiago eu não consegui avançar, pois eu não entendi. Porém, quero entender tudo o que você explicitou, peço que me corrija quando eu falhar e me ajude a avançar (por favor). O teorema binomial eu entendi. Sei que a soma dos coeficientes de um binômio

é dada por

(isso é bem observado no triângulo de Pascal, certo?). Mas o teorema multinomial eu não compreendi. Procurei alguma informação na internet, mas não consegui entender.
-
silviopuc
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Jan 15, 2013 12:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Seg Dez 30, 2013 18:28
por e8group » Seg Dez 30, 2013 18:28
Olá ,só quis deixar claro que é possível expandir

pelo teorema multinomial .Mas isto não importa ,só queremos a soma dos coeficiente de

na sua forma expandida .
Vamos supor que não conhecemos o teorema binomial e multinomial e queremos determinar a soma dos coeficientes de

e

nas suas formas expandida . Segue ,

E fazendo o mesmo processo acima sucessivas vezes esperamos que
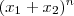
se exprima como

com
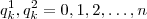
e

números reais . Quando fizemos
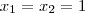
teremos a soma dos coeficientes
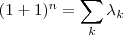
.
silviopuc escreveu: teorema binomial eu entendi. Sei que a soma dos coeficientes de um binômio é dada por (isso é bem observado no triângulo de Pascal, certo?)
Você estar certo .
Continuando ....
E forma análoga , podemos esperar que

se escreva como

(
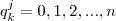
) e novamente se fizermos
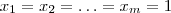
teremos a soma dos coeficientes que és

. No se exercício tente identificar o termo geral da soma . Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- trinômio
por cazevedo » Seg Abr 25, 2011 22:19
- 2 Respostas
- 2160 Exibições
- Última mensagem por cazevedo

Ter Abr 26, 2011 19:25
Polinômios
-
- (CESCEM-72) Trinômio
por aline2010 » Dom Jul 25, 2010 10:57
- 2 Respostas
- 2395 Exibições
- Última mensagem por agnesrava

Seg Mai 28, 2012 13:24
Álgebra Elementar
-
- Completando o trinomio
por Carlos28 » Qui Nov 08, 2012 08:19
- 2 Respostas
- 1504 Exibições
- Última mensagem por e8group

Qui Nov 08, 2012 09:26
Equações
-
- [FATORE O TRINÔMIO]
por mirikertty » Qua Dez 19, 2012 13:14
- 2 Respostas
- 2171 Exibições
- Última mensagem por joaofonseca

Sex Dez 21, 2012 22:00
Sistemas de Equações
-
- Trinômio Quadrado Perfeito
por Balanar » Ter Ago 10, 2010 22:48
- 2 Respostas
- 4920 Exibições
- Última mensagem por DanielFerreira

Dom Jan 08, 2012 18:05
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
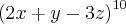 é necessariamente:
é necessariamente:
 e
e 

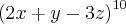 é necessariamente:
é necessariamente:
 e
e 

 .Esta soma a uma potência
.Esta soma a uma potência  se escreve como
se escreve como 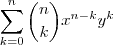 (Teorema Binomial ) e igualdade
(Teorema Binomial ) e igualdade  nos dá a soma dos coeficientes acima
nos dá a soma dos coeficientes acima 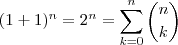 . E quando temos
. E quando temos  números reais
números reais  ,o teorema multinomial nos garanti uma forma de expandir
,o teorema multinomial nos garanti uma forma de expandir 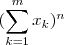 como se vê lá ...
como se vê lá ...  na sua forma expandida . Fazendo todos
na sua forma expandida . Fazendo todos  iguais a
iguais a  , teremos
, teremos  que és a soma requerida .
que és a soma requerida . se escreve sob a soma das parcelas que se exprimem por
se escreve sob a soma das parcelas que se exprimem por  ;
;  ,esta afirmação é assegurada pelo teorema multinomial , ou então notando a fórmula de recorrência :
,esta afirmação é assegurada pelo teorema multinomial , ou então notando a fórmula de recorrência :  .Em que a notação
.Em que a notação  designa a soma dos primeiros
designa a soma dos primeiros  termos da lista
termos da lista 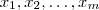 ,i.e.,
,i.e.,  .
. iguais
iguais  teremos a soma dos coeficientes
teremos a soma dos coeficientes  .
.
 é dada por
é dada por  (isso é bem observado no triângulo de Pascal, certo?). Mas o teorema multinomial eu não compreendi. Procurei alguma informação na internet, mas não consegui entender.
(isso é bem observado no triângulo de Pascal, certo?). Mas o teorema multinomial eu não compreendi. Procurei alguma informação na internet, mas não consegui entender.
 pelo teorema multinomial .Mas isto não importa ,só queremos a soma dos coeficiente de
pelo teorema multinomial .Mas isto não importa ,só queremos a soma dos coeficiente de  na sua forma expandida .
na sua forma expandida .  e
e  nas suas formas expandida . Segue ,
nas suas formas expandida . Segue , 
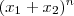 se exprima como
se exprima como  com
com 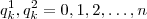 e
e  números reais . Quando fizemos
números reais . Quando fizemos 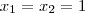 teremos a soma dos coeficientes
teremos a soma dos coeficientes 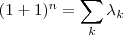 .
. se escreva como
se escreva como  (
(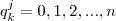 ) e novamente se fizermos
) e novamente se fizermos 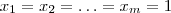 teremos a soma dos coeficientes que és
teremos a soma dos coeficientes que és  . No se exercício tente identificar o termo geral da soma . Tente concluir .
. No se exercício tente identificar o termo geral da soma . Tente concluir .





