anneliesero escreveu:a) Dividindo-se no universo racional o numero 123 pelo número 4, obtém-se quociente 3,75 .É VERDADEIRO não é mas no gabarito está FALSO
Se você dividir 123 por 4 vai obter 30,75. Esses são racionais, logo a divisão é possível e está dentro do conjunto citado.
anneliesero escreveu:b) No universo natural, o quociente da divisão do número 123 pelo número 4 é dez vezes o resíduo da divisão. É FALSO essa afirmativa?
Veja que
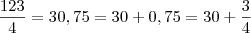
. O resíduo, portanto, da divisão é

que multiplicado por

iguala-se a parte inteira do quociente que é
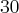
.
anneliesero escreveu:c) 10-6-2= 1+ 1 é óbvio que é VERDADEIRO não é?
Sim, é verdadeiro.

anneliesero escreveu:d) Sendo x um número real, tal que x<5 e x>3, podemos concluir que x=4. E Falso?
No universo Real existem infinitos números entre dois números quaisquer. Assim, não podemos determinar mais nada a cerca de

.
anneliesero escreveu:e) Sendo x e y números reais, tais que x<y, podemos concluir que -3x<-3y. Essa não entendi.
Se
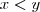
então

. Porém, quando multiplicamos a desigualdade pela unidade negativa (-1) temos de invertê-la. Isso, se deve ao fato de que, por exemplo:
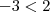
. Se multiplicarmos por -1 em ambos lados temos
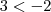
, que não é verdade. Assim, ao multiplicar a desigualdade por -1 temos de invertê-la:
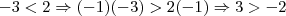
.
Logo, se
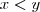
então

que implica em
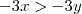
. Portanto, a afirmativa é falsa.
anneliesero escreveu:f) Sendo que a um número negativo, x e y números reais, tais que x>y, podemos concluir que a.x<a.y. Essa também não entendi.
Esta afirmativa é verdadeira. A justificativa segue na questão acima.




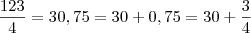 . O resíduo, portanto, da divisão é
. O resíduo, portanto, da divisão é  que multiplicado por
que multiplicado por  iguala-se a parte inteira do quociente que é
iguala-se a parte inteira do quociente que é 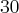 .
.
 .
.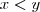 então
então  . Porém, quando multiplicamos a desigualdade pela unidade negativa (-1) temos de invertê-la. Isso, se deve ao fato de que, por exemplo:
. Porém, quando multiplicamos a desigualdade pela unidade negativa (-1) temos de invertê-la. Isso, se deve ao fato de que, por exemplo: 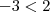 . Se multiplicarmos por -1 em ambos lados temos
. Se multiplicarmos por -1 em ambos lados temos 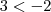 , que não é verdade. Assim, ao multiplicar a desigualdade por -1 temos de invertê-la:
, que não é verdade. Assim, ao multiplicar a desigualdade por -1 temos de invertê-la: 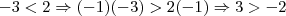 .
. 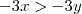 . Portanto, a afirmativa é falsa.
. Portanto, a afirmativa é falsa.

 .
.



