 por raimundoocjr » Dom Jun 09, 2013 19:22
por raimundoocjr » Dom Jun 09, 2013 19:22
Verificar
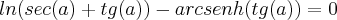
.
Qualquer ajuda é bem-vinda.
-
raimundoocjr
-
 por e8group » Dom Jun 09, 2013 21:54
por e8group » Dom Jun 09, 2013 21:54
Pela definição
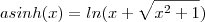
.Mas sabemos que
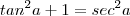
esta relação permite escrever
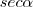
em função de
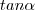
,com isso você obtêm que
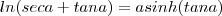
(Verifique !)
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- algebra l
por ehrefundini » Qui Mar 05, 2009 08:34
- 1 Respostas
- 7465 Exibições
- Última mensagem por Molina

Qui Mar 05, 2009 21:50
Álgebra
-
- algebra
por uspsilva » Sex Mar 13, 2009 13:03
- 1 Respostas
- 3211 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 15:22
Pedidos
-
- Algebra
por mattheusramos14 » Ter Ago 03, 2010 01:26
- 1 Respostas
- 2744 Exibições
- Última mensagem por MarceloFantini

Ter Ago 03, 2010 13:37
Álgebra Elementar
-
- ALGEBRA
por JOHNY » Sex Set 03, 2010 23:50
- 1 Respostas
- 2711 Exibições
- Última mensagem por MarceloFantini

Sáb Set 04, 2010 13:12
Álgebra Elementar
-
- álgebra
por Eliana Fidelis » Dom Out 24, 2010 13:52
- 1 Respostas
- 2652 Exibições
- Última mensagem por Adriano Tavares

Ter Mar 08, 2011 20:37
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
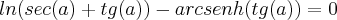 .
.
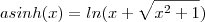 .Mas sabemos que
.Mas sabemos que 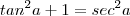 esta relação permite escrever
esta relação permite escrever 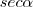 em função de
em função de 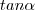 ,com isso você obtêm que
,com isso você obtêm que 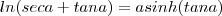 (Verifique !)
(Verifique !)
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)