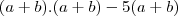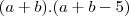por replay » Sex Mar 15, 2013 12:43
por replay » Sex Mar 15, 2013 12:43
Galera, fiquei com duvida nisso:

Usando a fórmula dos produtos notaveis cheguei em:


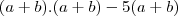
A partir daqui não sei resolver.
Editado pela última vez por
replay em Sex Mar 15, 2013 22:58, em um total de 2 vezes.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por timoteo » Sex Mar 15, 2013 19:21
por timoteo » Sex Mar 15, 2013 19:21
Olá.
Olha esse procedimento não existe:
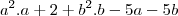
, a partir daqui está errado.
Recomendo que você retome algum livro de ensino médio que fale sobre o assunto, em especial na parte de propriedades da distribuição da multiplicação em relação a soma.
Eu gostaria de ver toda a questão se fosse possível!
Espero ter ajudado!
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por replay » Sex Mar 15, 2013 22:53
por replay » Sex Mar 15, 2013 22:53
Eu tentei ajustar , mais ja vi o que está errado.
Grato.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por replay » Dom Mar 17, 2013 23:55
por replay » Dom Mar 17, 2013 23:55
Ajustei minha nova tentativa, alguêm pode ajudar?
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por timoteo » Seg Mar 18, 2013 18:09
por timoteo » Seg Mar 18, 2013 18:09
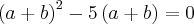
Multiplicando ambos lados por
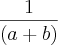
fica: a + b - 5 = 0 --> a + b = 5.
Caso existam valores que não foram colocados no enunciado, esta resposta pode não ser a verdadeira. Imagino que haja algo faltando no enunciado!
Espero ter ajudado!
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por replay » Qua Mar 20, 2013 00:47
por replay » Qua Mar 20, 2013 00:47
Timóteo.
Obrigado pela ajuda.
Mas realmente não tem enunciado, apenas o professor pediu que fatorasse.
Não tenho experiência nesse tipo de fatoração.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por replay » Qui Mar 21, 2013 10:17
por replay » Qui Mar 21, 2013 10:17
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por timoteo » Qui Mar 21, 2013 12:23
por timoteo » Qui Mar 21, 2013 12:23
Sim!
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida na Fatoração
por runksoneck » Sáb Fev 19, 2011 18:30
- 2 Respostas
- 4359 Exibições
- Última mensagem por runksoneck

Ter Fev 22, 2011 09:57
Pedidos
-
- dúvida fatoração
por Andrewo » Ter Mar 13, 2012 16:51
- 5 Respostas
- 2804 Exibições
- Última mensagem por LuizAquino

Qua Mar 28, 2012 17:19
Álgebra Elementar
-
- Fatoração - Dúvida
por Danilo » Sáb Mar 09, 2013 12:16
- 1 Respostas
- 1431 Exibições
- Última mensagem por e8group

Sáb Mar 09, 2013 13:16
Álgebra Elementar
-
- Fatoração - dúvida
por laura_biscaro » Sex Mar 15, 2013 01:06
- 3 Respostas
- 2077 Exibições
- Última mensagem por DanielFerreira

Dom Mar 17, 2013 18:57
Álgebra Elementar
-
- [Fatoração] Dúvida em exercício
por Antonio Unwisser » Sáb Ago 30, 2014 21:36
- 3 Respostas
- 2281 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 21:22
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



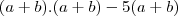




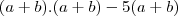

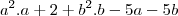 , a partir daqui está errado.
, a partir daqui está errado.


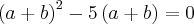
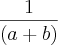 fica: a + b - 5 = 0 --> a + b = 5.
fica: a + b - 5 = 0 --> a + b = 5.