 por rodrigonapoleao » Seg Nov 19, 2012 16:28
por rodrigonapoleao » Seg Nov 19, 2012 16:28
como acho a soluçao do conjunto |x-1|>|x|?
-
rodrigonapoleao
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Nov 19, 2012 14:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por MarceloFantini » Seg Nov 19, 2012 23:25
por MarceloFantini » Seg Nov 19, 2012 23:25
Primeiro, não existe solução de um conjunto. Neste caso é o
conjunto solução da inequação.
Para resolvê-la, precisa considerar os casos
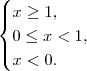
No primeiro teremos
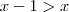
.
No segundo teremos
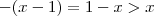
.
No terceiro teremos
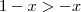
Note então que no primeiro caso não existe solução, pois -1 é menor, e não maior, que zero. Logo não existem soluções maiores ou iguais a um.
No segundo caso encontramos que
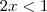
e
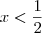
. Como
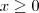
, segue que a solução será
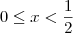
.
Por último, sabemos que

sempre, logo todo
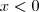
é solução.
Unindo as respostas chegamos em
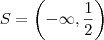
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



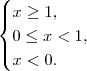
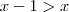 .
.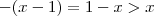 .
.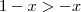
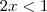 e
e 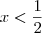 . Como
. Como 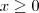 , segue que a solução será
, segue que a solução será 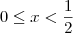 .
. sempre, logo todo
sempre, logo todo 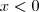 é solução.
é solução.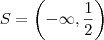 .
.



 , avisa que eu resolvo.
, avisa que eu resolvo.

