 por Balanar » Seg Ago 30, 2010 05:56
por Balanar » Seg Ago 30, 2010 05:56
Observe abaixo a semi-reta orientada e um segmento de medida 1. Determine o ponto desse segmento inicial (x), tal que ele seja média geométrica do segmento inicial e do segmento restante
................................................................> Reais positivos
0----------------x------1
Resposta:
x=(-1+raiz de 5)/2
Olha pra ser sincero a única coisa que sei e que a média geométrica é:
raiz enésima do produto de x.
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Douglasm » Seg Ago 30, 2010 19:00
por Douglasm » Seg Ago 30, 2010 19:00
Neste caso, nós temos que interpretar o problema da seguinte forma: a média geométrica entre o segmento inicial (
1 u) e o restante do segmento, após ser determinado nele um ponto x (
1-x u), tem um valor igual ao desse ponto. Ou seja:


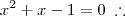

* Note que a raiz negativa não nos interessa, haja vista que não pertence ao segmento pedido.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Balanar » Seg Ago 30, 2010 19:04
por Balanar » Seg Ago 30, 2010 19:04
Excelente Resposta.
VLW
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- <=====Números Complexos-Média Geométrica=====>
por futuromilitar » Qui Mai 26, 2016 22:08
- 1 Respostas
- 11076 Exibições
- Última mensagem por DanielFerreira

Ter Mai 31, 2016 00:44
Números Complexos
-
- [Progressao] série geometrica X progressao geometrica?
por aajunim » Seg Mar 18, 2013 11:19
- 2 Respostas
- 4245 Exibições
- Última mensagem por aajunim

Ter Mar 19, 2013 11:44
Progressões
-
- P.A - Média
por DanielFerreira » Qua Jul 29, 2009 15:30
- 2 Respostas
- 2660 Exibições
- Última mensagem por DanielFerreira

Qui Jul 30, 2009 17:27
Progressões
-
- média
por Andreza » Qui Nov 24, 2011 13:03
- 3 Respostas
- 2606 Exibições
- Última mensagem por Neperiano

Sex Nov 25, 2011 10:15
Estatística
-
- média
por Italo de Souza » Sáb Out 11, 2014 11:09
- 4 Respostas
- 6843 Exibições
- Última mensagem por jcmatematica

Dom Out 12, 2014 02:27
Teoria dos Números
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




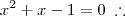


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
