Sejam , a,b,c, d números primos distintos e seja x um número primo que divide o número abcd.
Prove que x é diferente de a,b ,c , d.
por MarceloFantini » Qua Jul 14, 2010 15:32
por Molina » Qua Jul 14, 2010 21:39
, que é diferente dos números pegos no exemplo.
por Douglasm » Qui Jul 15, 2010 13:30
por Tom » Sex Jul 16, 2010 00:54
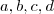, existe um primo 
, diferente dos supracitados, que divide o número 
por ckde » Sáb Jul 17, 2010 13:01
um número primo que divide o número 
, é ab + cd e não abcdpor Douglasm » Sáb Jul 17, 2010 13:17
por Molina » Sáb Jul 17, 2010 14:12
Douglasm escreveu:Então "ab" e "cd" são produtos? Se for assim é fácil. Note que ab+cd não é divisível por nenhum deles (dito que a, b, c e d são primos). Por exemplo:
O mesmo vale para b, c e d. Logo, é evidente que, se ab+cd não é divisível por qualquer dos primos supracitados, ele é divisível por, pelo menos, um outro primo x.
ckde escreveu:Sejam , a,b,c, d números primos distintos e seja x um número primo que divide o número ab+cd.
Prove que x é diferente de a,b ,c , d.
por Tom » Sáb Jul 17, 2010 14:13
ckde escreveu:Desculpem, realmente ficou difícil sem usar o LaTeX... A questão tem um errinho. O certo é: seja
por ckde » Sáb Jul 17, 2010 22:23
por mony0771 » Qui Abr 23, 2009 10:54
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a e elevar ao quadrado os dois lados)