 por Jacques » Sex Set 02, 2016 22:24
por Jacques » Sex Set 02, 2016 22:24
Bem, não sei onde deveria postar isso, é uma dúvida em uma questão de Calculo I, mas é uma dúvida básica de decidir postar aqui. Peço perdão se estiver equivocado
- A questão pede para construir o gráfico da seguinte função.
f(x) = 3x? + 4x³ - 36x² + 29
e estou com dificuldades para achar as raízes onde x= 0
por indução eu descobri que umas das raízes é X¹=1, basta substituir e verificar. Dividindo por ( x -1 ) é o obtido a função --> g(x) = 3x³ + 7x² - 29x - 29. Se eu achar as 3 desse eu consigo resolver.
R=As outras raízes que verifiquei com um software de gráfico são -> X²(-0.88,0) X³(2.66,0) X?(-4.11,0)
-
Jacques
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Jul 12, 2016 21:18
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por adauto martins » Sáb Set 10, 2016 14:41
por adauto martins » Sáb Set 10, 2016 14:41
o polinomio em questao tem os coeficientes de num.inteiros,entao existira pelo menos uma raiz racional
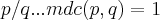
,onde

e

...entao o conj. da possivel ou possiveis raizes racionais saira do conj.{

}...o intervalo onde essas raizes estarao e dado por:

,q. no nosso caso sera
![\rho =1+ 36/3=13\Rightarrow {I}_{s}=[-13,13] \rho =1+ 36/3=13\Rightarrow {I}_{s}=[-13,13]](/latexrender/pictures/16a708bb807494ceacfe6500e78a82c6.png)
,ou seja todos os possiveis num. do conj. podem ser raiz do polinomio...como vc verificou q. 1 é raiz ou seja
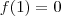
e fatorou em

...agora fazer o mesmo processo com

,pois

,ai vai baixando grau do polinomio,q. é quarto grau,foi pra terceiro e assim sucessivamente...esse polinomio

,pode ter uma raiz racional e um conjudado de raizes complexas ou as tres raizes racionais...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [fatoração] fatoração de polinômio do quarto grau.
por +Danilo2 » Qui Set 29, 2016 10:43
- 5 Respostas
- 8899 Exibições
- Última mensagem por +Danilo2

Sáb Out 08, 2016 18:17
Polinômios
-
- fatoração de Polinômio fatoração de agrupamento
por Estudante13 » Sex Nov 09, 2012 22:52
- 1 Respostas
- 3251 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 23:06
Álgebra Elementar
-
- Fatoração de Polinômio
por Gobate » Dom Nov 21, 2010 01:50
- 1 Respostas
- 1911 Exibições
- Última mensagem por OtavioBonassi

Qua Jan 05, 2011 21:38
Polinômios
-
- Fatoração e raízes de um polinômio
por pablohas » Qua Dez 08, 2010 21:26
- 2 Respostas
- 3757 Exibições
- Última mensagem por Elcioschin

Sex Dez 10, 2010 22:05
Polinômios
-
- [polinômio]Relações de Girard + raízes de polinômio
por matano2104 » Qui Set 05, 2013 17:02
- 1 Respostas
- 7150 Exibições
- Última mensagem por young_jedi

Qui Set 05, 2013 17:57
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


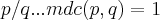 ,onde
,onde  e
e  ...entao o conj. da possivel ou possiveis raizes racionais saira do conj.{
...entao o conj. da possivel ou possiveis raizes racionais saira do conj.{ }...o intervalo onde essas raizes estarao e dado por:
}...o intervalo onde essas raizes estarao e dado por: ,q. no nosso caso sera
,q. no nosso caso sera ![\rho =1+ 36/3=13\Rightarrow {I}_{s}=[-13,13] \rho =1+ 36/3=13\Rightarrow {I}_{s}=[-13,13]](/latexrender/pictures/16a708bb807494ceacfe6500e78a82c6.png) ,ou seja todos os possiveis num. do conj. podem ser raiz do polinomio...como vc verificou q. 1 é raiz ou seja
,ou seja todos os possiveis num. do conj. podem ser raiz do polinomio...como vc verificou q. 1 é raiz ou seja 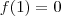 e fatorou em
e fatorou em  ...agora fazer o mesmo processo com
...agora fazer o mesmo processo com  ,pois
,pois  ,ai vai baixando grau do polinomio,q. é quarto grau,foi pra terceiro e assim sucessivamente...esse polinomio
,ai vai baixando grau do polinomio,q. é quarto grau,foi pra terceiro e assim sucessivamente...esse polinomio 
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.