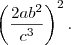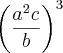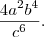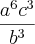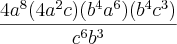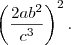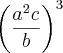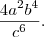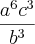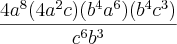por Jem - » Dom Jan 24, 2010 16:58
por Jem - » Dom Jan 24, 2010 16:58
Olá
Estou com algumas duvidas na seguinte questao
Efetue as operações :
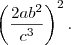
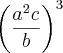
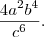
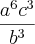
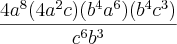
E agora..como continuo?, cancelo expoentes?/
não sei cmo devo proceder, se puderem me ajudar...
-
Jem -
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Dez 26, 2009 18:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Seg Jan 25, 2010 09:46
por Elcioschin » Seg Jan 25, 2010 09:46
Esqueça a última linha do seu raciocínio
(4*a²*b^4)*(a^6*c³)/c^6*b³ ----> Apenas junte os termos do numerador:
4*a^8*b^4*c³/c^6*b³ ----> Simplifique b^4 com b³ e c³ com c^6
4*a^4*b/c³
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3686 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
-
- Potência de potência... não sei ao certo se entendi...
por Vennom » Sáb Fev 20, 2010 10:42
- 3 Respostas
- 3769 Exibições
- Última mensagem por mottasky

Ter Out 04, 2011 02:03
Álgebra Elementar
-
- [Potencia] soma de potencia com letras
por carla villela » Qui Mar 01, 2012 21:04
- 8 Respostas
- 8604 Exibições
- Última mensagem por carla villela

Qui Mar 01, 2012 22:18
Sistemas de Equações
-
- Potenciação - Potência de potência
por Ana Paula MMS » Sáb Jan 11, 2014 14:59
- 1 Respostas
- 2631 Exibições
- Última mensagem por Cleyson007

Sáb Jan 11, 2014 17:27
Aritmética
-
- (Potencia) equação com potencia
por Thiago1986Iz » Dom Jul 24, 2016 12:53
- 1 Respostas
- 2038 Exibições
- Última mensagem por DanielFerreira

Dom Jul 24, 2016 16:00
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.