 por Kah » Qua Mar 18, 2015 17:44
por Kah » Qua Mar 18, 2015 17:44
Olá! Alguém pode me ajudar, por favor?
Como simplifico essa fração algébrica?
Sei que no numerador tenho uma diferença entre quadrados e no denominador um diferença entre cubos. Fiz assim:
Numerador:
m³ - 1 = (m - 1)(m² + m + 1)
Denominador
m^6 - 1 = (m²)³ - (1)³ = (m² - 1)(m^4 + m² + 1) = [(m + 1)(m - 1)]( m^4 + m² + 1 )
Simplifiquei (m - 1) do numerador com o (m - 1) do denominador, ficando assim:
(m² + m + 1)/ (m + 1)( m^4 + m² + 1 )
Não consigo sair disso :/
O que fiz de errado?
- Anexos
-

- Mat.png (3.53 KiB) Exibido 2159 vezes
-
Kah
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Mar 18, 2015 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Qua Mar 18, 2015 22:38
por Russman » Qua Mar 18, 2015 22:38
Pensei uma forma mais direta.
Se você tomar
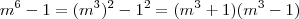
Daí,
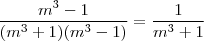
Mas você não fez errado.
Note que se você dividir

obterá
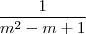
e, portanto, o resultado será

.
Para dividir os polinômios basta observar seus graus. Já que o polinômio do numerador é de grau 2 e do denominador de grau 4 então o quaociente entre eles será um polinômio de grau zero dividido por um de grau 2.
Daí, suponha que existam reais a, b e c tais que

Sem dificuldades você concluirá que
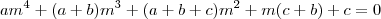
de onde a=1, b=-1 e c=1 por igualdade de polinômios.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Soma de frações algébricas, como igualar os denominadores?
por lucas7 » Qui Fev 17, 2011 20:55
- 5 Respostas
- 4209 Exibições
- Última mensagem por Cleyson007

Sex Fev 18, 2011 18:23
Álgebra Elementar
-
- frações algebricas
por tamirosa » Qui Out 29, 2009 20:11
- 1 Respostas
- 3309 Exibições
- Última mensagem por Molina

Sex Out 30, 2009 11:37
Álgebra Elementar
-
- Frações Algébricas
por LuizCarlos » Dom Ago 07, 2011 21:45
- 5 Respostas
- 2932 Exibições
- Última mensagem por MarceloFantini

Seg Ago 08, 2011 02:06
Álgebra Elementar
-
- Frações Algébricas
por LuizCarlos » Qui Abr 19, 2012 14:33
- 4 Respostas
- 2192 Exibições
- Última mensagem por LuizCarlos

Qui Abr 19, 2012 17:59
Álgebra Elementar
-
- Frações Algébricas Ajudem-me!
por Jansen » Seg Ago 31, 2009 23:32
- 0 Respostas
- 1675 Exibições
- Última mensagem por Jansen

Seg Ago 31, 2009 23:32
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


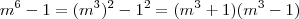
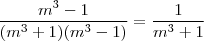
 obterá
obterá 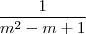 e, portanto, o resultado será
e, portanto, o resultado será .
.
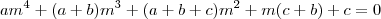



 , avisa que eu resolvo.
, avisa que eu resolvo.

