 por Cleyson007 » Sáb Ago 24, 2013 00:20
por Cleyson007 » Sáb Ago 24, 2013 00:20
Seja
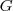
um grupo e

. Sabendo-se que a ordem de

é 2, a ordem de

é 3 e

, determine a ordem de
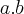
.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Renato_RJ » Sáb Ago 24, 2013 00:47
por Renato_RJ » Sáb Ago 24, 2013 00:47
Cleyson007 escreveu:Seja
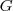
um grupo e

. Sabendo-se que a ordem de

é 2, a ordem de

é 3 e

, determine a ordem de
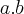
.
Boa noite !!!
Vejamos, G é um grupo abeliano (pois

), os elementos a e b possuem ordem finita (O(a) = 2 e O(b) = 3) e o MDC (O(a),O(b)) = 1 (MDC(2,3) = 1) então O(ab) = O(a)O(b), logo a ordem de a.b = 6 (isso é uma proposição vinda do Teorema de Cauchy).
Abraços...
Editado pela última vez por
Renato_RJ em Sáb Ago 24, 2013 17:56, em um total de 1 vez.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Cleyson007 » Sáb Ago 24, 2013 11:13
por Cleyson007 » Sáb Ago 24, 2013 11:13
Renato, estava pensando por aqui e acho que a resposta também poderia ser dada pelo Teorema de Lagrange. O que acha?
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Renato_RJ » Sáb Ago 24, 2013 14:42
por Renato_RJ » Sáb Ago 24, 2013 14:42
Cleyson007 escreveu:Renato, estava pensando por aqui e acho que a resposta também poderia ser dada pelo Teorema de Lagrange. O que acha?
Pode sim, mas eu acho que é "dar tiro de canhão para matar mosquito"....
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Outra ED.
por Higor » Seg Fev 21, 2011 15:52
- 2 Respostas
- 1980 Exibições
- Última mensagem por Higor

Seg Fev 21, 2011 17:04
Cálculo: Limites, Derivadas e Integrais
-
- Outra - fração
por cidaiesbik » Qui Mai 21, 2009 10:35
- 3 Respostas
- 3553 Exibições
- Última mensagem por cidaiesbik

Seg Mai 25, 2009 10:17
Desafios Enviados
-
- Outra Dúvida
por rodsales » Sáb Jun 06, 2009 21:41
- 1 Respostas
- 1493 Exibições
- Última mensagem por Marcampucio

Sáb Jun 06, 2009 22:38
Trigonometria
-
- Outra dúvida
por rodsales » Qui Jun 18, 2009 22:12
- 1 Respostas
- 1432 Exibições
- Última mensagem por Marcampucio

Sex Jun 19, 2009 00:48
Trigonometria
-
- Outra dúvida.
por rodsales » Seg Out 12, 2009 09:56
- 1 Respostas
- 1505 Exibições
- Última mensagem por Marcampucio

Seg Out 12, 2009 11:59
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
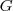 um grupo e
um grupo e  . Sabendo-se que a ordem de
. Sabendo-se que a ordem de  é 2, a ordem de
é 2, a ordem de  é 3 e
é 3 e  , determine a ordem de
, determine a ordem de 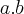 .
.
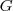 um grupo e
um grupo e  . Sabendo-se que a ordem de
. Sabendo-se que a ordem de  é 2, a ordem de
é 2, a ordem de  é 3 e
é 3 e  , determine a ordem de
, determine a ordem de 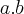 .
.
um grupo e
. Sabendo-se que a ordem de
é 2, a ordem de
é 3 e
, determine a ordem de
.
 ), os elementos a e b possuem ordem finita (O(a) = 2 e O(b) = 3) e o MDC (O(a),O(b)) = 1 (MDC(2,3) = 1) então O(ab) = O(a)O(b), logo a ordem de a.b = 6 (isso é uma proposição vinda do Teorema de Cauchy).
), os elementos a e b possuem ordem finita (O(a) = 2 e O(b) = 3) e o MDC (O(a),O(b)) = 1 (MDC(2,3) = 1) então O(ab) = O(a)O(b), logo a ordem de a.b = 6 (isso é uma proposição vinda do Teorema de Cauchy).



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)