 por 380625 » Sex Jul 05, 2013 15:18
por 380625 » Sex Jul 05, 2013 15:18
Qual a maneira correta de decompor a função

em fração parciais pois ja tentei de alguns modos e não consegui. Onde a é uma constante positiva.
Ficaria grato com a ajuda.
Flávio Santana.
-
380625
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sex Fev 18, 2011 17:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por young_jedi » Sex Jul 05, 2013 17:51
por young_jedi » Sex Jul 05, 2013 17:51
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por young_jedi » Sáb Jul 06, 2013 20:46
por young_jedi » Sáb Jul 06, 2013 20:46
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por 380625 » Sáb Jul 13, 2013 00:33
por 380625 » Sáb Jul 13, 2013 00:33
Entao mas assim onde está o outro termo pois o exercicio pede para mostrar que
![L^-1 \Big[\dfrac{s}{(s^2+a^2)^2}\Big] = \dfrac{1}{2a^3}\sin at - \dfrac{1}{2a^2} t \cos at} L^-1 \Big[\dfrac{s}{(s^2+a^2)^2}\Big] = \dfrac{1}{2a^3}\sin at - \dfrac{1}{2a^2} t \cos at}](/latexrender/pictures/afccd0c6afe9f5dc84fcaa2a02891972.png)
Note que na sua resposta não da isso.
Eu derivei f(s) e encontrei o mesmo que vc. Como chego na resposta correta.
Grato
Flávio Santana.
-
380625
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sex Fev 18, 2011 17:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por young_jedi » Sáb Jul 13, 2013 10:41
por young_jedi » Sáb Jul 13, 2013 10:41
Então ainda não vi uma maneira de se chegar nesta resolução que você colocou, vou continuar pensando se tiver alguma evolução eu posto aqui.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- frações parciais
por fasaatyro » Qui Dez 04, 2014 09:18
- 1 Respostas
- 1146 Exibições
- Última mensagem por lucas_carvalho

Qui Dez 04, 2014 11:28
Cálculo: Limites, Derivadas e Integrais
-
- Integral por Frações Parciais
por Bruhh » Qua Set 29, 2010 18:20
- 2 Respostas
- 5397 Exibições
- Última mensagem por Bruhh

Qui Set 30, 2010 08:40
Cálculo: Limites, Derivadas e Integrais
-
- [integral] fraçoes parciais
por ewald » Qui Set 08, 2011 15:10
- 1 Respostas
- 2112 Exibições
- Última mensagem por Neperiano

Qui Set 08, 2011 15:47
Cálculo: Limites, Derivadas e Integrais
-
- integrais por frações parciais
 por engrangel » Qua Abr 18, 2012 15:46
por engrangel » Qua Abr 18, 2012 15:46
- 2 Respostas
- 2935 Exibições
- Última mensagem por engrangel

Qui Abr 19, 2012 17:47
Cálculo: Limites, Derivadas e Integrais
-
- integral frações parciais
por paolaads » Seg Out 22, 2012 21:08
- 3 Respostas
- 2470 Exibições
- Última mensagem por MarceloFantini

Ter Out 23, 2012 18:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 em fração parciais pois ja tentei de alguns modos e não consegui. Onde a é uma constante positiva.
em fração parciais pois ja tentei de alguns modos e não consegui. Onde a é uma constante positiva.
 em fração parciais pois ja tentei de alguns modos e não consegui. Onde a é uma constante positiva.
em fração parciais pois ja tentei de alguns modos e não consegui. Onde a é uma constante positiva.



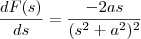


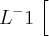
![\dfrac{s}{(s^2+a^2)^2}\right\Big] \dfrac{s}{(s^2+a^2)^2}\right\Big]](/latexrender/pictures/9ca1e7d76b5d77b82b13fb3ead55e473.png) =
=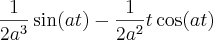

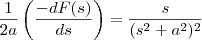
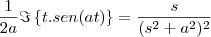


![L^-1 \Big[\dfrac{s}{(s^2+a^2)^2}\Big] = \dfrac{1}{2a^3}\sin at - \dfrac{1}{2a^2} t \cos at} L^-1 \Big[\dfrac{s}{(s^2+a^2)^2}\Big] = \dfrac{1}{2a^3}\sin at - \dfrac{1}{2a^2} t \cos at}](/latexrender/pictures/afccd0c6afe9f5dc84fcaa2a02891972.png)

